Daftar Isi
- Grafik Untuk Melihat Ditribusi Data
- Grafik Untuk Melihat Beda Distribusi Data Antar Grup
- Grafik Untuk Memvisualisasikan Korelasi Antar Variabel
- Grafik Yang Digunakan Untuk Memvisualisasikan Asosiasi Antar Variabel
- Grafik Yang Digunakan Untuk Memisualisasikan Ukuran Sampel dan Perubahan Sepanjang Waktu
Pada Chapter 4 dan 5 kita telah belajar bagaimana cara membuat grafik menggunakan R. Sejauh ini kita belum belajar kegunaan dari masing-masing grafik yang telah kita pelajarai. Pada Chapter ini kita tidak lagi akan membahas bagaimana membuat grafik menggunakan R. Kita akan fokus terhadap fungsi grafik tersebut dalam analisa kita. Secara umum grafik dibuat untuk memvisualisasikan distribusi, perbedaan antar sampel, korelasi dan asosiasi antar sampel, serta ukuran sampel.
Penulis dan pembaca pasti sepakat bahwa visualisasi data merupakan tahapan awal yang perlu kita lakukan sebelum memutuskan untuk melakukan analisa data seperti uji hipotesis dan modeling. Angka yang ditampilkan dalam ringkasan data tidaklah cukup untuk melihat data terutama kaitannya dengan pengecekan terhadap asumsi model.
Pada Gambar 1 disajikan delapan buah scatterplot dengan koefisien korelasi yang sama persis. Komputasi statistik tanpa melihat pada visualisasi data akan menyebabkan misinterpretasi pada data. Grafik memberikan ringkasan visual data dengan cepat dan lengkap dibandingkan penyajian data dalam tabel angka.
## Warning: package 'knitr' was built under R version 3.5.3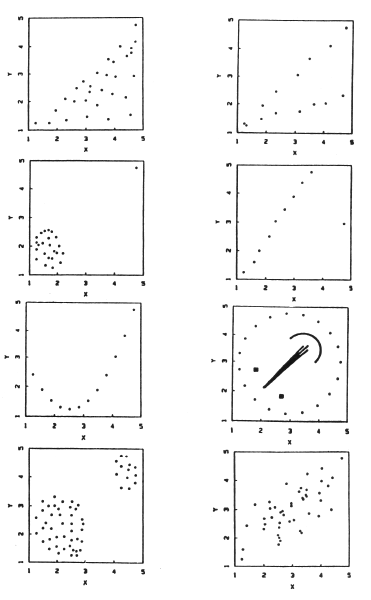
Figure 1: Scatterplot dengan koefisien korelasi r=0,7.
Grafik sangat penting untuk dua tujuan:
- untuk memberikan wawasan bagi analis ke dalam data di bawah pengawasan, dan
- untuk mengilustrasikan konsep-konsep penting ketika mempresentasikan hasil kepada orang lain.
Tugas pertama disebut Analisis Data Eksplorasi (EDA), dan merupakan subjek Chapter ini. Prosedur EDA seringkali merupakan (atau seharusnya) menjadi ‘pandangan pertama’ pada data. Pola dan teori tentang bagaimana sistem berperilaku dikembangkan dengan mengamati data melalui grafik. Ini adalah prosedur induktif - data dirangkum dibanding dilakukan pengujian. Hasil mereka memberikan panduan untuk pemilihan prosedur pengujian hipotesis deduktif yang tepat.
Setelah analisis selesai, temuan harus dilaporkan kepada orang lain. Apakah laporan tertulis atau presentasi lisan, analis harus meyakinkan audiens bahwa kesimpulan yang dicapai didukung oleh data. Tidak ada cara yang lebih baik untuk melakukan ini selain melalui grafik. Banyak metode grafis yang sama yang merangkum informasi dengan ringkas untuk analis juga akan memberikan wawasan tentang data untuk pembaca atau audiens.
7.1 Grafik Untuk Melihat Ditribusi Data
Analisis yang umumnya dilihat pada distribusi data adalah apakah data berdistribusi normal atau tidak. Hal ini akan mempengaruhi jenis analisis statistika yang digunakan pada data. Terdapat beberapa grafik yang dapat digunakan untuk melihat bentuk ditribusi data. Grafik-grafik tersebut antara lain: stem and leaf, histogram, density plot, QQ-plot, serta box plot atau violin plot. Pada analisis distribusi stem and leaf kurang populer untuk digunakan. Hal ini disebabkan karena visualisasinya kurang cocok diterapkan pada data dengan jumlah observasi besar. Selain itu, kita juga tidak bisa melakukan perbandingan antar grup menggunakan jenis visualisasi tersebut.
7.1.1 Histogram
Histogram adalah grafik yang sudah dikenal, dan konstruksinya dirinci dalam berbagai teks pengantar tentang statistik. Batang digambar dengan tinggi ni, atau fraksi ni/n, dari data yang termasuk dalam salah satu dari beberapa kategori atau interval (Gambar 2). Iman dan Conover (1983) mengemukakan bahwa untuk ukuran sampel n, jumlah interval k harus bilangan bulat terkecil sehingga 2k≥n.
Histogram sangat berguna untuk menggambarkan perbedaan besar dalam bentuk data seperti apakah data simetris seperti distribusi normal atau memiliki kemencengan. Histogram tidak dapat digunakan untuk penilaian yang lebih tepat karena tampilan dipengaruhi oleh jumlah batang yang digunakan. Untuk lebih memahaminya perhatikan Gambar 2 dan Gambar 3. Kedua histogram tersebut tampak berbeda meskipun data input yang diberikan sama. Pada Gambar 2 kita akan melihat bahwa debit dengan kejadian terbanyak terjadi pada rentang 800-900 cfs, sedangkan pada Gambar 3 kita melihat bahwa debit dengan kejadian terbanyak terjadi pada 800-1200 cfs.
# memuat library
library(readxl)## Warning: package 'readxl' was built under R version 3.5.3library(ggplot2)
library(ggthemes)## Warning: package 'ggthemes' was built under R version 3.5.3# memuat data excel
sungai <- read_excel("hhappc.xls", sheet="appc1")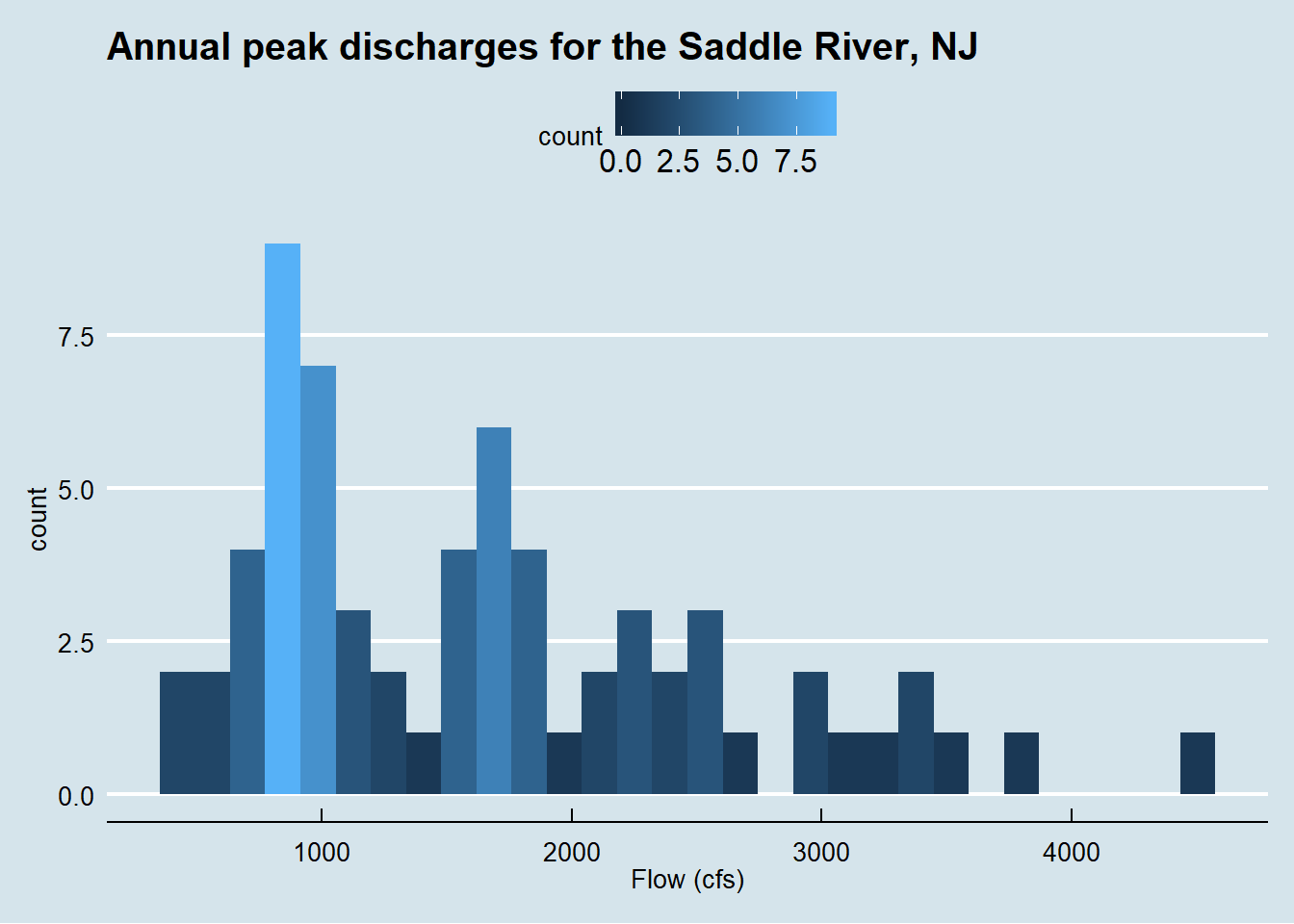
Figure 2: Histogram dengan bin.width=default debit sungai Saddle
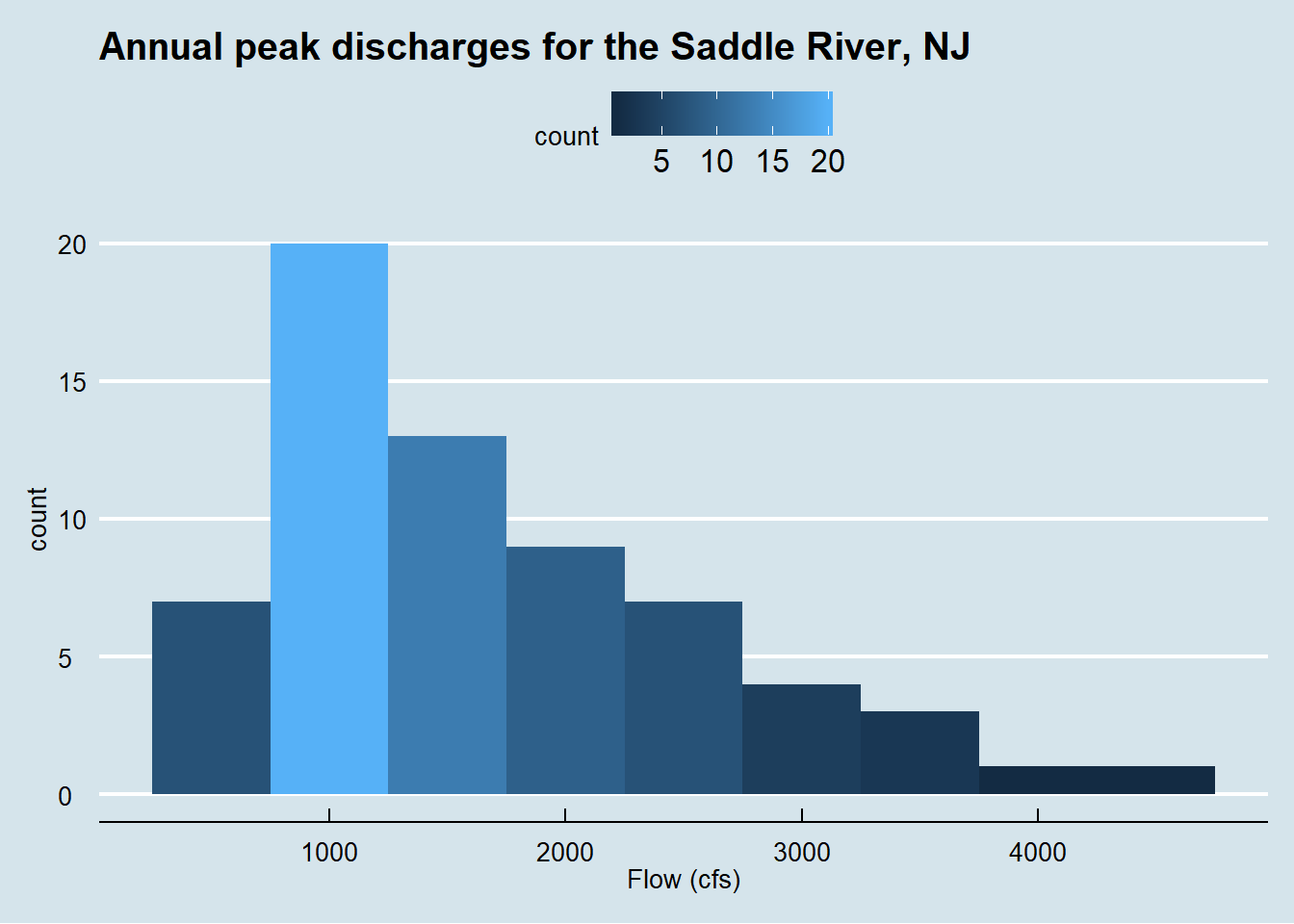
Figure 3: Histogram dengan bin.width=500 debit sungai Saddle
7.1.2 Density Plot
Density plot memecahkan masalah yang dimiliki histogram dalam melihat grafik dengan menyajikan data bukan dari jumlah kejadian atau observasi, namun data disajikan berdasarkan frekuensi relatif data (density) yang digambarkan dalam bentuk smooth curve. Contoh density plot dapat dilijat pada Gambar 4. Dari grafik yang dihasilkan sekaran tampak jelas bahwa distibusi data memiliki kemencengan positif dengan frekuensi relatif debit terbanyak berada pada debit 1000 cfs.
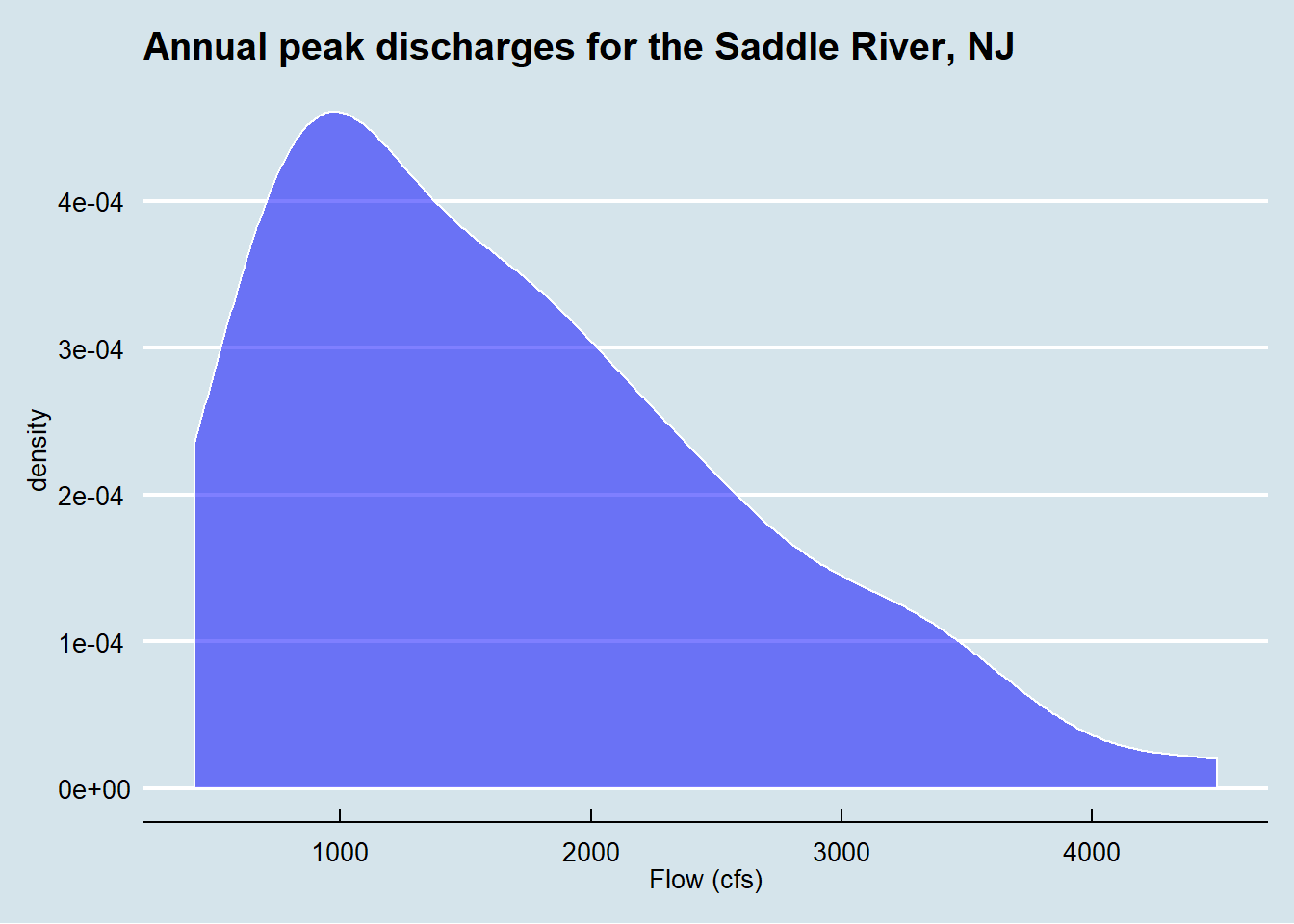
Figure 4: Density plot debit sungai Saddle
7.1.3 QQ-plot
Kita telah mempelajari sebelumnya pada Chapter 5 bahwa QQ-plot data digunakan untuk mengecek apakah data yang kita miliki berdistribusi normal atau tidak. Contoh QQ-plot dapat dilijat pada Gambar 5. Pada grafik yang dihasilkan terlihat bahwa data tidak berdistribusi normal. Hal ini terlihat dari sebagian observasi pada debit <1000 cfs yang tidak mengikuti garis referensi.
ggplot(sungai, aes(sample=Flow))+
# qq plot
stat_qq()+
# garis referensi
stat_qq_line()+
theme_economist()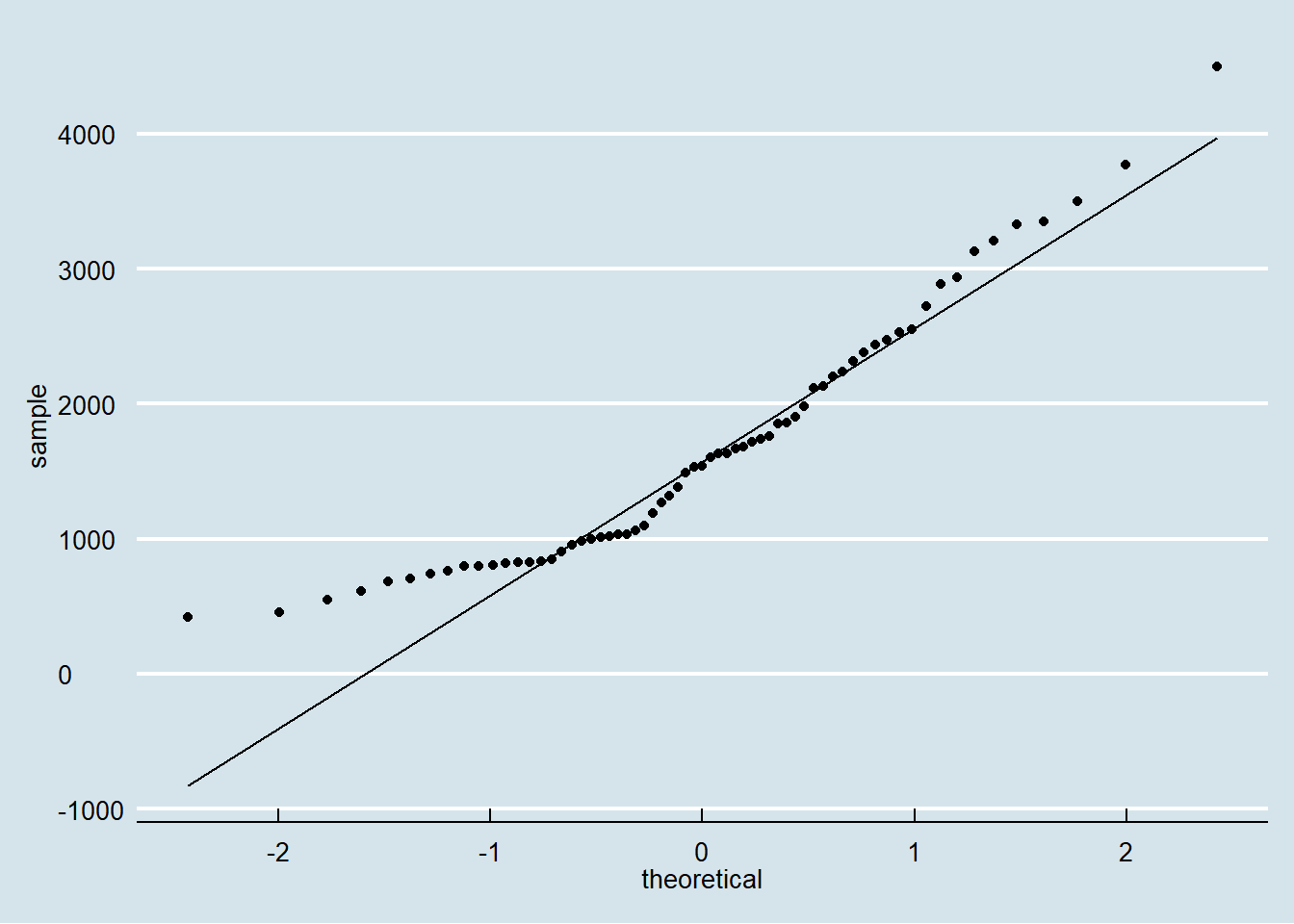
Figure 5: QQ plot debit sungai Saddle
7.1.4 Box Plot dan Violin Plot
Grafik lain yang dapat digunakan untuk menggambarkan distribusi data adalah box plot dan violin plot. Box plot memberikan cara yang simpel untuk melihat ditribusi data seperti melihat posisi sejumlah kuartil, nilai minimum dan maksimum. Selain itu kita juga dapat melihat adanya outlier pada data.
Kita dapat menambah fungsionalitas dari box plot ini dengan menambahkan violin plot. Pada Chapter 5 kita telah belajar bahwa kita dapat menambahkan box plot pada violin plot atau sebaliknya sehingga memudahkan dalam mendeskripsikan bentuk distribusi data. Jika dengan box plot kita tidak dapat melihat secara baik bentuk dari data yang sesungguhnya karena hanya menampilkan lokasi sejumlah kuartil. Pada violin plot kita dapat melihat bentuk data yang ada melalui tampilan dua denisty plot (tampak seperti biola) yang digambarkan. Kekurangannya adalah kita tidak dapat melihat observasi mana yang menjadi outlier, sehingga kedua grafik ini biasa digambarkan secara bersamaan. Berikut adalah contoh box plot dan violin plot dari data debit sungai Saddle (Gambar 6).
ggplot(sungai, aes(x="", y=Flow))+
geom_violin(fill="blue", alpha=0.5, color="white")+
geom_boxplot(width=0.1)+
theme_economist()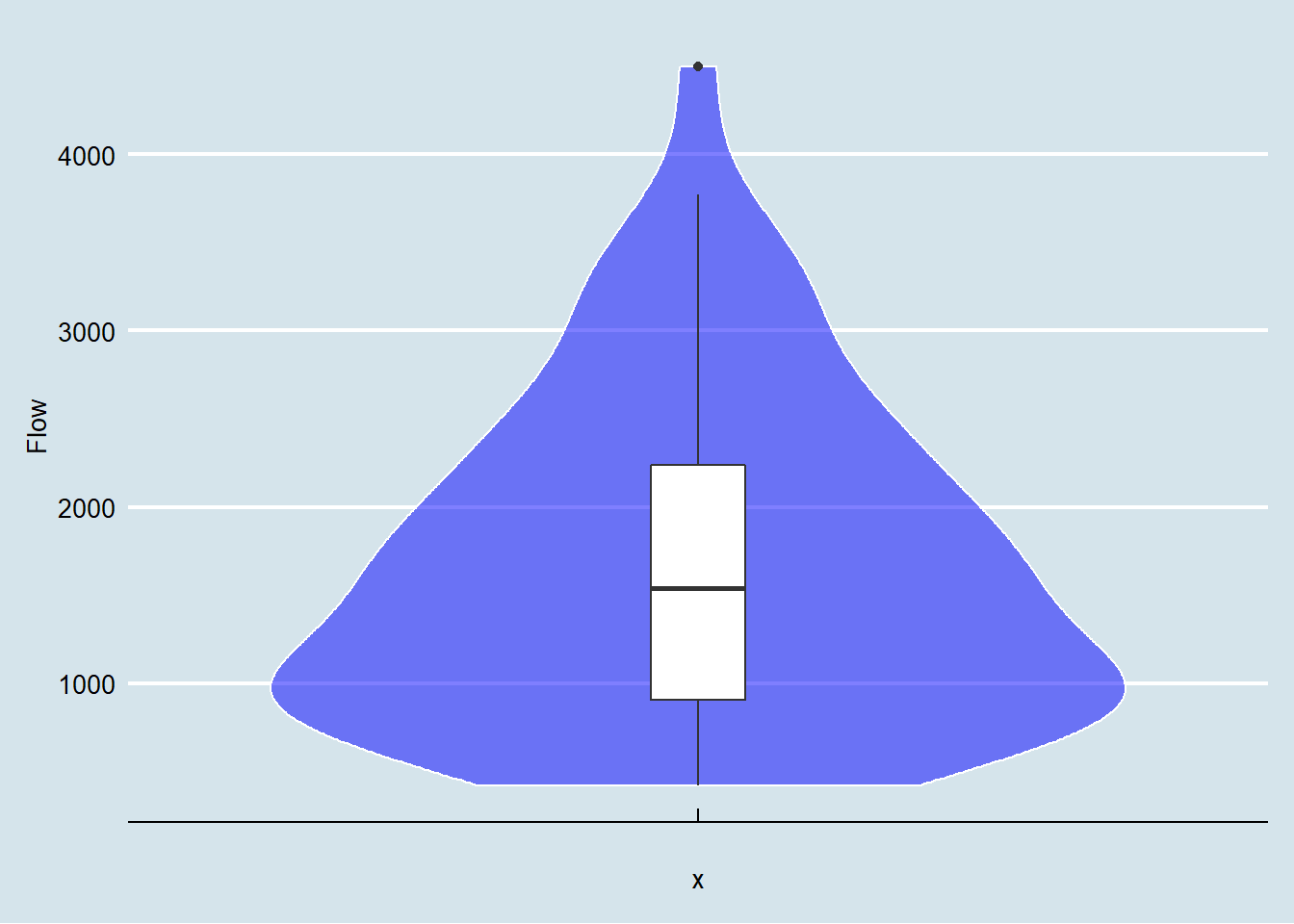
Figure 6: Box plot dan violin plot debit sungai Saddle
Berdasarkan grafik yang dihasilkan pada Gambar 6 kita dapat melihat bahwa ditribusi data debit sungai memiliki kemencengan positif. Hal ini terjadi karena terdapat satu outlier pada data yang disebabkan karena nilai observasinya diluar dari nilai maksimum data yang ditetapkan sebagai max=Q3+1,5∗IQR.
7.2 Grafik Untuk Melihat Beda Distribusi Data Antar Grup
Grafik yang telah dijelaskan sebelumnya seperti box plot, violin plot, histogram, dan density plot merupakan grafik yang bagus untuk memvisualisasikan beda distribusi data antar grup untuk data numerik. Untuk data berupa kategori kita dapat menggunakan bar plot. Pada penerapannya bar plot juga dapat memvisualisasikan ringkasan data seperti nilai mean dan sebarannya pada data.
Pada contoh ini penulis hanya akan memberikan contoh penerapan menggunakan box plot dan bar plot menggunakan data konsentrasi Antrazine yang diukur pada bulan Juni dan September. Untuk melakukannya kita perlu memuat data dan melakukan transformasi terhadap datanya terlebih dahulu.
# memuat data excel
atrazine <- read_excel("hhappc.xls", sheet="appc4")
# print
head(atrazine)## # A tibble: 6 x 2
## June_atrazine Sept_atrazine
## <dbl> <dbl>
## 1 0.38 2.66
## 2 0.04 0.63
## 3 -0.01 0.59
## 4 0.03 0.05
## 5 0.03 0.84
## 6 0.05 0.580# transformasi data
library(tidyr)## Warning: package 'tidyr' was built under R version 3.5.3atrazine <- gather(atrazine,
key="month",
value="concentration")
# print
head(atrazine)## # A tibble: 6 x 2
## month concentration
## <chr> <dbl>
## 1 June_atrazine 0.38
## 2 June_atrazine 0.04
## 3 June_atrazine -0.01
## 4 June_atrazine 0.03
## 5 June_atrazine 0.03
## 6 June_atrazine 0.05Pada data konsentrasi Atrazine tersebut terdapat nilai negatif yang dalam hal ini merupakan kesalahan dalam pengukuran dari alat. Untuk membersihkannya kita dapat membuat nilai observasi tersebut menjadi NA.
atrazine$concentration[atrazine$concentration<0]<-NA
head(atrazine)## # A tibble: 6 x 2
## month concentration
## <chr> <dbl>
## 1 June_atrazine 0.38
## 2 June_atrazine 0.04
## 3 June_atrazine NA
## 4 June_atrazine 0.03
## 5 June_atrazine 0.03
## 6 June_atrazine 0.05Selanjutnya kita akan memvisualisasikan beda antara distribusi data pada kedua bulan menggunakan box plot (Gambar 7). Konsentrasi rata-rata Atrazine akan divisualisasikan menggunakan bar plot (Gambar 8).
ggplot(atrazine, aes(month, concentration, fill=month))+
geom_boxplot()+
theme_economist()+
scale_fill_economist()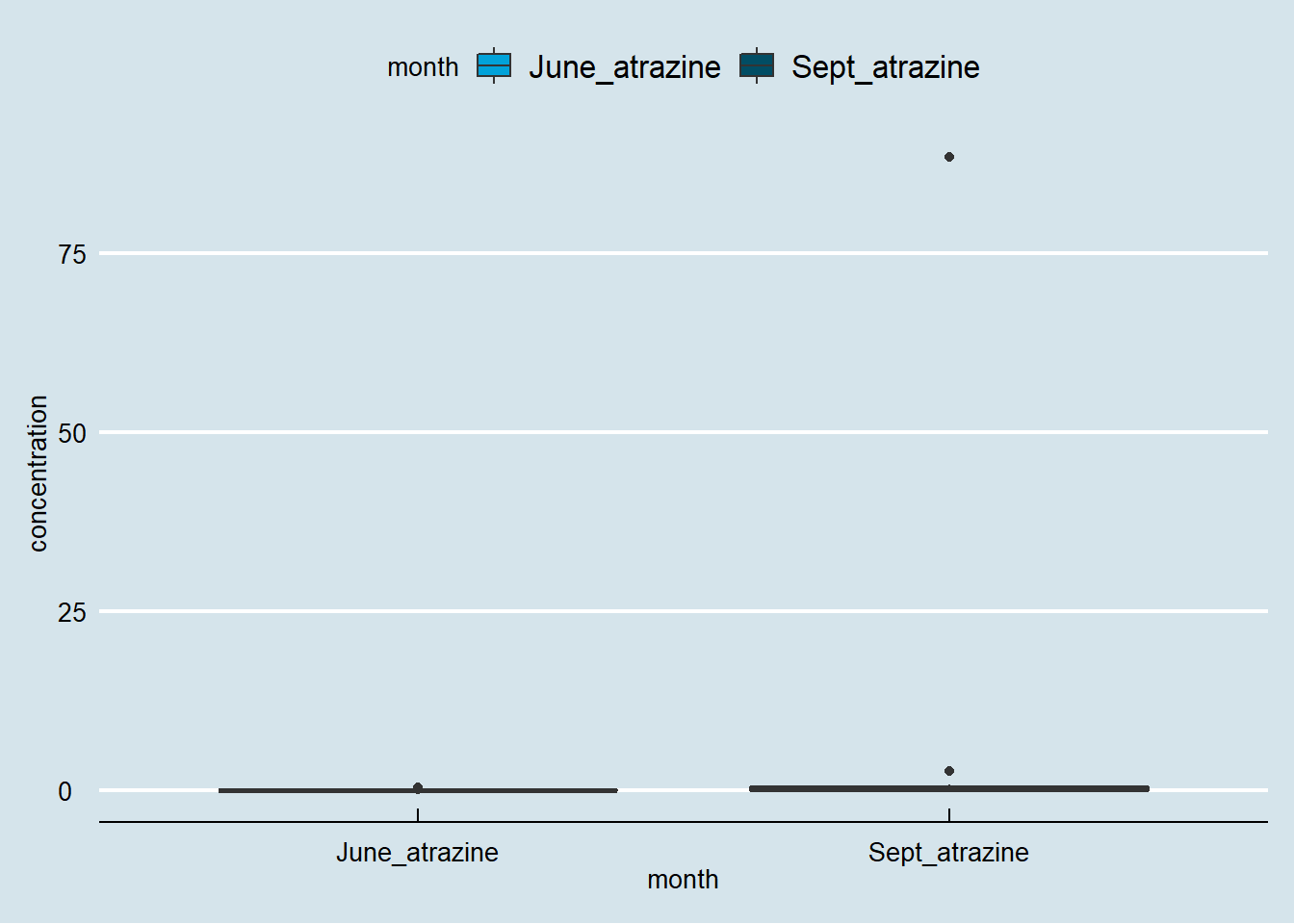
Figure 7: Box plot konsentrasi Atrazine pada bulan Juni dan September
library(dplyr)
atrazine %>%
group_by(month) %>%
summarize(mean_atrazine=mean(concentration, na.rm=TRUE)) %>%
ggplot(aes(month, mean_atrazine, fill=month))+
geom_bar(stat="identity")+
theme_economist()+
scale_fill_economist()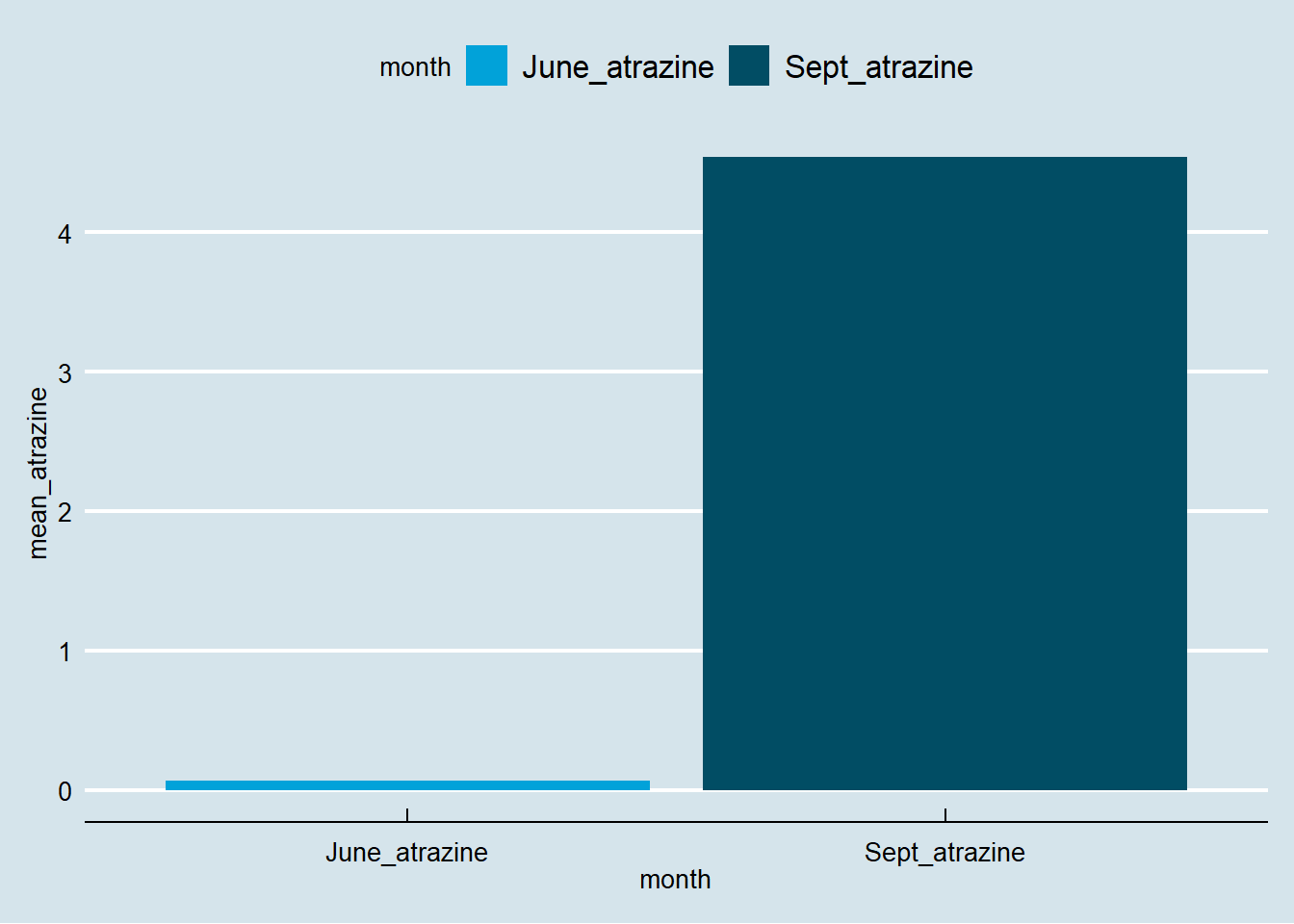
Figure 8: Bar plot konsentrasi Atrazine pada bulan Juni dan September
Pada visualisasi yang dihasilkan terdapat perbedaan signifikan antara distribusi dan nilai rata-rata konsentrasi Atrazine pada dua periode tersebut. Hal ini disebabkan karena terdapat sebuah outlier pada periode Sepetember yang menyebabkan nilai rata-rata yang dihasilkan bergeser jauh kearah outlier. Pembaca dapat membuat visualisasi data pada data tersebut tanpa outlier dengan terlebih dahulu melakukan filter terhadap outlier.
7.3 Grafik Untuk Memvisualisasikan Korelasi Antar Variabel
Scatterplot dapat digunakan untuk memvisualisasikan korelasi antar dua variabel. Pada bagian ini akan diberikan contoh visualisasi antara variabel konsentrasi TDS dan Uranium pada air tanah.
Untuk melakukannya kita perlu memuat terlebih dahulu dataset yang digunakan. Visualisasi data disajikan pada Gambar 9.
# memuat data excel
gw <- read_excel("hhappc.xls", sheet="appc16")ggplot(gw, aes(TDS, Uranium))+
geom_point()+
geom_smooth(method="lm")+
theme_economist()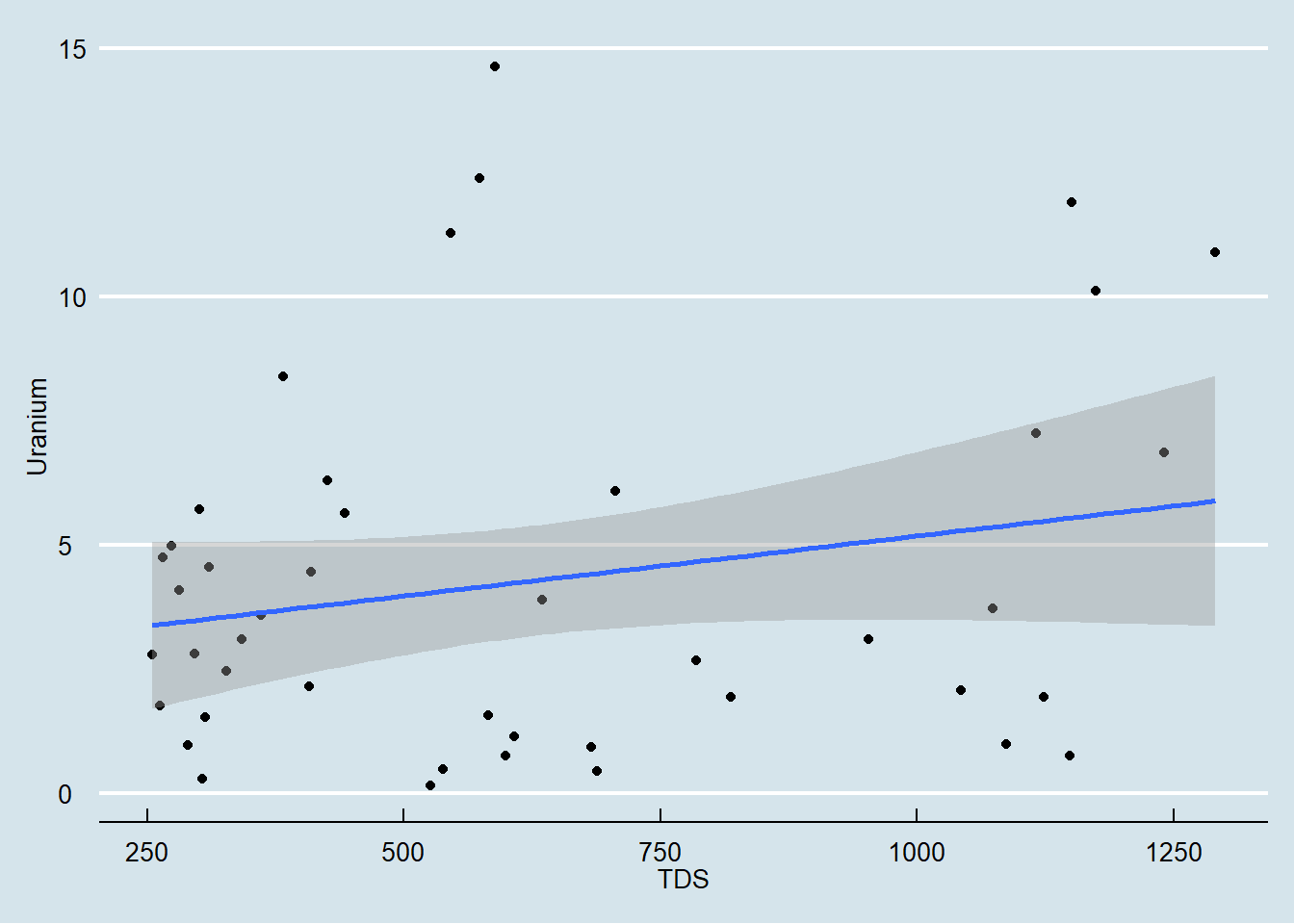
Figure 9: Scatterplot hubungan antara konsentrasi TDS dan Uranium pada airtanah
Berdasarkan grafik yang dihasilkan terdapat hubungan linier antara konsentrasi TDS dan Uranium pada airtanah. Meningkatnya konsentrasi TDS pada air tanah juga menyebabkan peningkatan konsentrasi Uranium pada airtanah.
7.4 Grafik Yang Digunakan Untuk Memvisualisasikan Asosiasi Antar Variabel
Asosiasi antar variabel kategori dapat dilakukan baik dengan pie chart maupun dengan bar plot. Pie chart kurang sering digunakan untuk visualisasi multiple group sehingga bar plot lebih sering digunakan.
Pada contoh kali ini penulis akan melihat terdapat asoiasi antara musim dan strata terhadap jumlah Corbicula di sungai Tennessee. Untuk melakukannya kita perlu memuat terlebih dahulu dataset yang digunakan. Visualisasi data disajikan pada Gambar 10.
# memuat data excel
corbicula<- read_excel("hhappc.xls", sheet="appc8")
# print
head(corbicula)## # A tibble: 6 x 4
## Year Season Strata Corbicula
## <dbl> <chr> <dbl> <dbl>
## 1 1969 Winter 1 25
## 2 1969 Winter 1 20
## 3 1969 Winter 1 30
## 4 1969 Spring 1 9
## 5 1969 Spring 1 8
## 6 1969 Spring 1 9corbicula %>%
mutate(Season=as.factor(Season),
Strata=as.factor(Strata)) %>%
group_by(Season,Strata) %>%
summarize(Corbicula=mean(Corbicula)) %>%
ggplot(aes(Season, Corbicula, fill=Strata))+
geom_bar(stat="identity",position=position_dodge2())+
theme_economist()+
scale_fill_economist()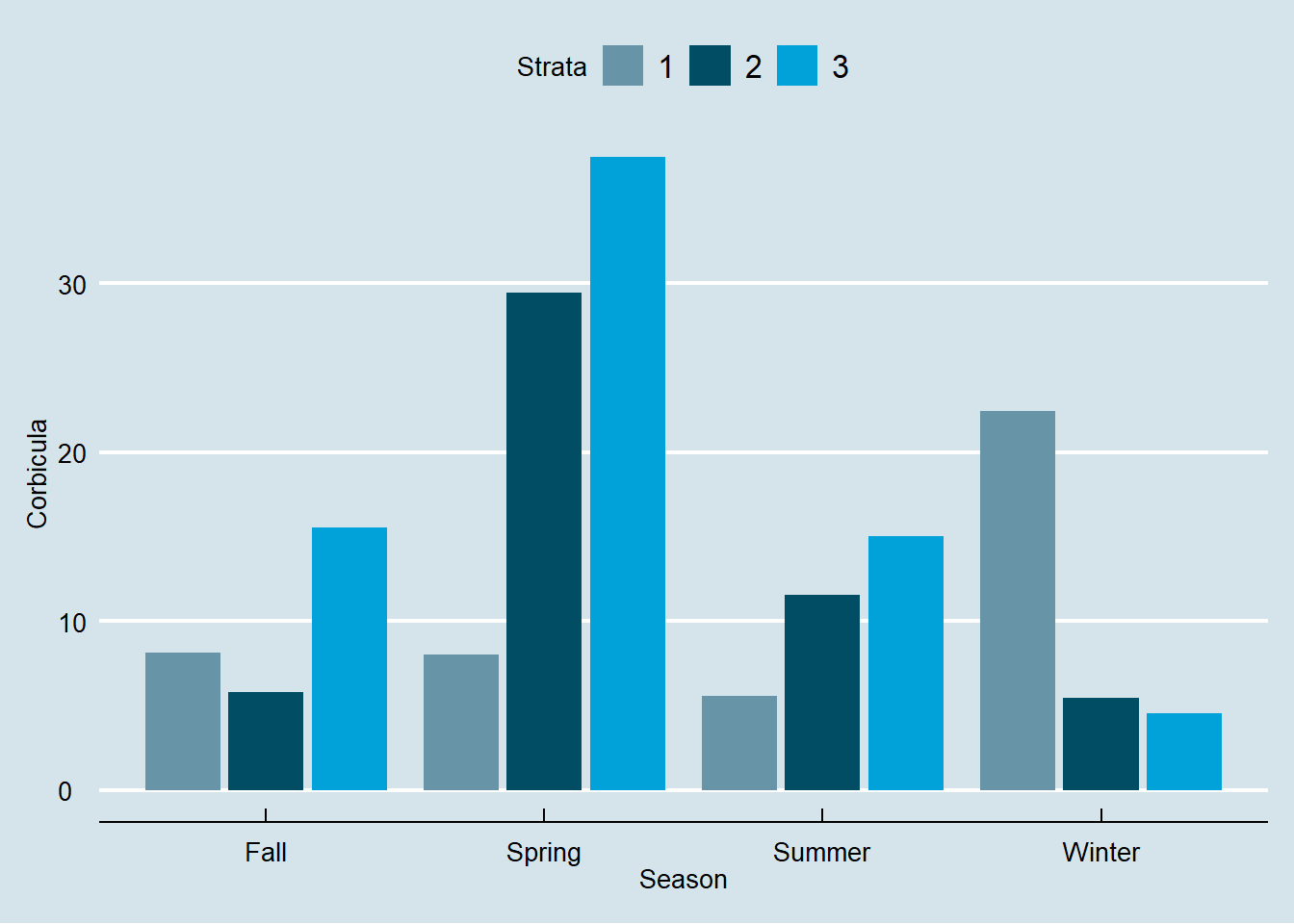
Figure 10: Bar plot Jumlah rata-rata corbicula pada sungai Tennessee
Berdasarkan grafik yang dihasilkan terdapat pengaruh musim dan strata terhadap jumlah corbicula di sungai Tennessee. Jumlah tertinggi berada saat musim semi pada strata 3, sedangkan terendah berada pada musim dingin juga pada strata 3.
7.5 Grafik Yang Digunakan Untuk Memisualisasikan Ukuran Sampel dan Perubahan Sepanjang Waktu
Untuk memvisualisasikan perubahan sepanjang waktu, kita dapat menggunakan line plot. Pada data corbicula kita ingin memvisualisasikan perubahan jumlah corbicula rata-rata pada setiap tahun. Visualisasi dari data disajikan pada Gambar 11.
corbicula %>%
group_by(Year) %>%
summarize(Corbicula=mean(Corbicula)) %>%
ggplot(aes(Year, Corbicula))+
geom_line()+
geom_point(shape=1)+
theme_economist()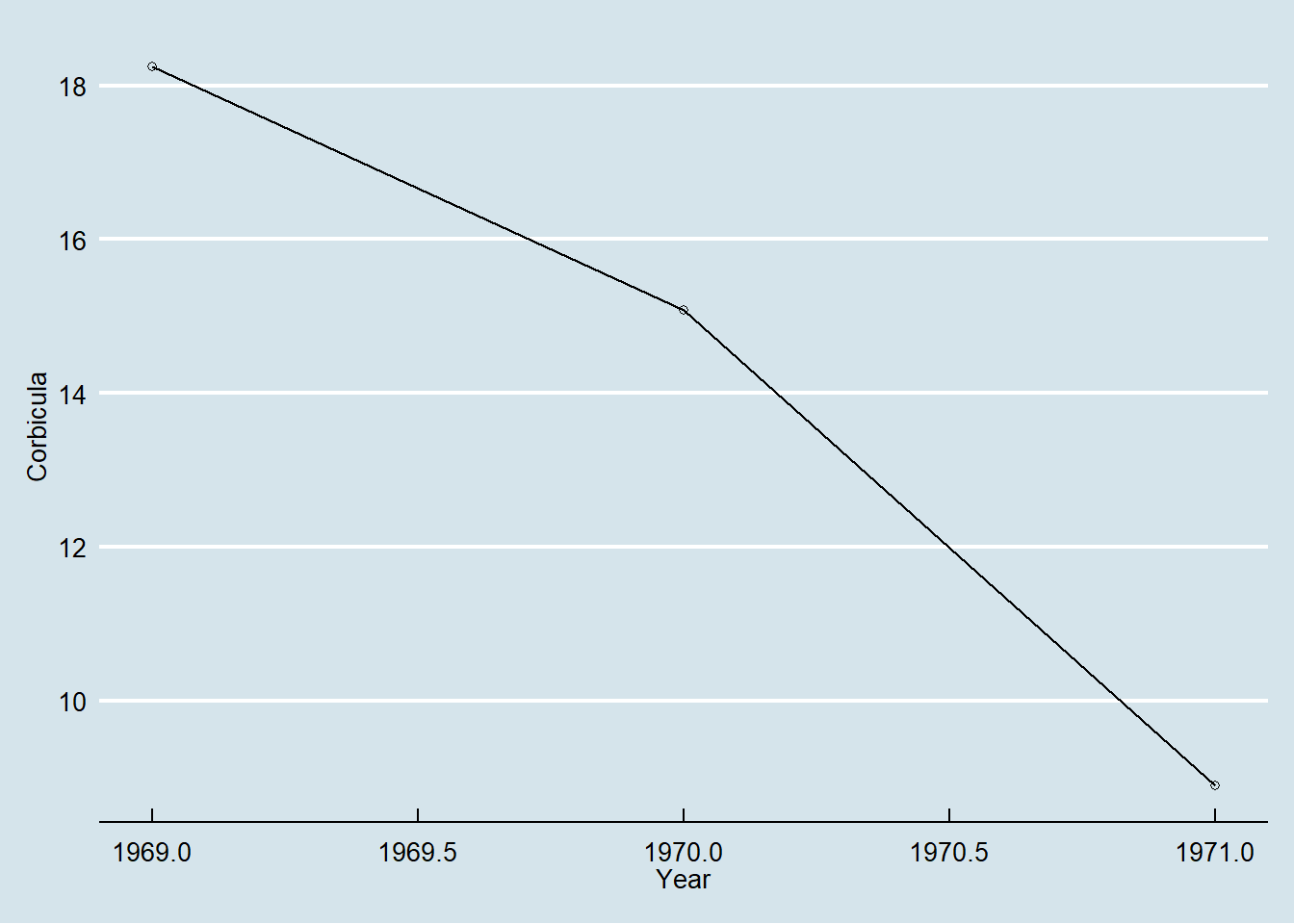
Figure 11: Line plot perubahan jumlah rata-rata corbicula di sungai Tennessee
Berdasarkan garfik yang dihasilkan dapat disimpulkan bahwa jumlah rata-rata corbicula menurun setiap tahunnya.
Referensi
- Gardener, M. 2012. Statistics for Ecologists Using R and Excel-Data collection, exploration, analysis and presentation. Pelagic Publishing.
- Helsel, D.R., Hirsch, R.M. 2002. statistical Methods in Water Resources. USGS.
- Ofungwu, J. 2014. Statistical Applications For Environmental Analysis and Risk Assessment. John Wiley & Sons, Inc.
- Peck, R.Devore, J.L. 2012. Statistics The Exploration & Analysis of Data- Seventh Edition. Brooks/Cole.