Daftar Isi
- Definisi Interval Estimasi
- Interpretasi Interval Estimasi
- Interval Kepercayaan Median
- Interval Kepercayaan Mean
- Interval Prediksi Nonparametrik
- Transformasi DataInterval Prediksi Parametrik
- Interval Kepercayaan Persentil (Interval Toleransi)
- Interval Kepercayaan Menggunakan Metode Bootstrap
- Kegunaan Lain Dari Interval Kepercayaan
Pada Chapter 6-Ringkasan Numerik kita telah belajar beberapa atribut kunci dari data seperti \(\overline{X}\) dan \(s\). Kedua nilai tersebut disebut sebagai nilai estimasi sampel dari populasi (untuk mean \(\mu\) dan simpangan baku \(\sigma\)). Pada Chapter ini kita akan melakukan eksplorasi lebih jauh lagi mengenai interval estimasi (interval estimate) yang akan menyinggung kedua nilai tersebut lebih jauh.
10.1 Definisi Interval Estimasi
Median sampel dan mean sampel menyatakan titik pemusatan data. Estimasi menggunakan kedua nilai tersebut disebut sebagai estimasi titik (point estimation). Estimasi titik sendiri tidak menggambarkan reliabilitas atau kurangnya reliabilitas (variabilitas) dari estimasi ini. Sebagai contoh, anggaplah terdapat dua data X dan Y dengan mean 5 dengan jumlah observasi yang sama. Data Y memiliki nilai mean 5 dengan sangat sedikit variasi didalamnya, sedangkan data X jauh lebih bervariasi. Perkiraan titik 5 untuk X jauh lebih tidak dapat diandalkan dibandingkan dengan untuk Y karena variabilitas yang lebih besar dalam data X. Dengan kata lain, lebih banyak kehati-hatian diperlukan ketika menyatakan bahwa 5 memperkirakan mean populasi sebenarnya X daripada ketika menyatakan ini untuk Y. Melaporkan hanya perkiraan mean sampel (poin) 5 gagal memberikan petunjuk tentang perbedaan ini.
Sebagai alternatif untuk estimasi titik, estimasi interval adalah interval yang memiliki probabilitas yang dinyatakan mengandung nilai populasi sebenarnya. interval lebih lebar untuk set data yang memiliki variabilitas lebih besar. Jadi dalam contoh di atas, interval antara 4,7 dan 5,3 mungkin memiliki kemungkinan 95% untuk mengandung mean populasi Y yang sebenarnya (tidak diketahui). Butuh interval yang jauh lebih luas, katakanlah antara 2,0 dan 8,0, untuk memiliki probabilitas yang sama untuk mengandung rerata sebenarnya dari X. Karena itu, perbedaan keandalan dari dua estimasi dengan jelas dinyatakan menggunakan estimasi interval. Estimasi interval dapat memberikan dua informasi yang estimasi poin tidak dapat berikan, antara lain:
- Pernyataan probabilitas atau kemungkinan bahwa interval berisi nilai populasi sebenarnya (keandalannya).
- Pernyataan kemungkinan bahwa satu titik data dengan besaran tertentu berasal dari populasi yang diteliti.
Estimasi interval untuk poin pertama disebut sebagai interval kepercayaan (confidence interval), sedangkan yang kedua disebut sebagai interval prediksi (prediction interal). Meskipun salin terkait, pembaca perlu berhati-hati sebab kedua definisi tersebut sering kali tertukar satu sama lain.
10.2 Interpretasi Interval Estimasi
Untuk lebih memahami mengenai definisi interval estimasi pada sub-chapter ini akan diberikan contoh yang diambil dari buku statistical Methods in Water Resources karya Helsel dan Hirsch (2012). Misalkan mean populasi sebenarnya \(\mu\) konsentrasi dalam akuifer adalah 10. Sleain itu, anggaplah bahwa varians populasi sebenarnya \(\sigma^2\) sama dengan 1. Karena nilai-nilai ini dalam praktiknya tidak pernah diketahui, sampel diambil untuk memperkirakannya dengan mean sampel \(x\) dan sampel varian \(s^2\) . Dana yang cukup tersedia untuk mengambil 12 sampel air (kira-kira satu per bulan) selama satu tahun, dan hari-hari di mana pengambilan sampel terjadi dipilih secara acak. Dari 12 sampel ini \(x\)x dan \(s^2\) dihitung. Meskipun pada kenyataannya hanya satu set 12 sampel akan diambil setiap tahun, menggunakan komputer 12 hari dapat dipilih beberapa kali untuk menggambarkan konsep perkiraan interval. Untuk masing-masing dari 10 set independen dari 12 sampel, interval kepercayaan pada mean dihitung dengan menggunakan persamaan yang diberikan pada Tabel 1 dan Gambar 1.
| No. | N | Mean | St.Dev | 90% Interval kepercayaan |
|---|---|---|---|---|
| 1 | 12 | 10,06 | 1,11 | 9,46 sampai 10,64 |
| 2 | 12 | 10,60 | 0,81 | \(^+\) 10,18 sampai 11,02 |
| 3 | 12 | 9,95 | 1,26 | 9,29 sampai 10,60 |
| 4 | 12 | 10,18 | 1,26 | 9,52 sampai 10,83 |
| 5 | 12 | 10,17 | 1,33 | 9,48 sampai 10,85 |
| 6 | 12 | 10,22 | 1,19 | 9,60 sampai 10,84 |
| 7 | 12 | 9,71 | 1,51 | 8,92 sampai 10,49 |
| 8 | 12 | 9,90 | 1,01 | 9,38 sampai 10,43 |
| 9 | 12 | 9,95 | 0.10 | 9,43 sampai 10,46 |
| 10 | 12 | 9,88 | 1,37 | 9,17 sampai 10,59 |
Kesepuluh interval pada contoh di atas disebut dengan dengan interval kepercayaan 90% dari nilai mean sesungguhnya. Nilai mean sebenarnya akan terdapat pada interval tersebut dengan probabilitas 90%. Sehingga berdasarkan Tabel 1 terdapat 9 interval yang memiliki nilai mean sesungguhnya didalamnya (probabilitas 90%). Jika kita sekali lagi melakukan sampling dengan jumlah sampling yang sama pada interval nilai baru yang dihasilkan akan mengandung nilai mean sesungguhnya dan dapat juga tidak. Probabilitas interval tersebut mengandung nilai mean sesungguhnya disebut sebagai tingkat kepercayaan (confidence level). Probabilitas nilai interval tidak mengandung mean sesungguhnya disebut sebagai alpha level (\(\alpha\)) yang ditulis berdasarkan Persamaan (1).
\[\begin{equation} \alpha=1-confidence\ level\ \tag{1} \end{equation}\]Lebar interval kepercayaan adalah fungsi dari bentuk distribusi data (variabilitas dan kemencengannya), ukuran sampel, dan tingkat kepercayaan yang diinginkan. Ketika tingkat kepercayaan meningkat, lebar interval juga meningkat, karena interval yang lebih besar lebih mungkin mengandung nilai sebenarnya daripada interval yang lebih pendek. Dengan demikian interval kepercayaan 95% akan lebih luas daripada interval 90% untuk data yang sama.
## Warning: package 'knitr' was built under R version 3.5.3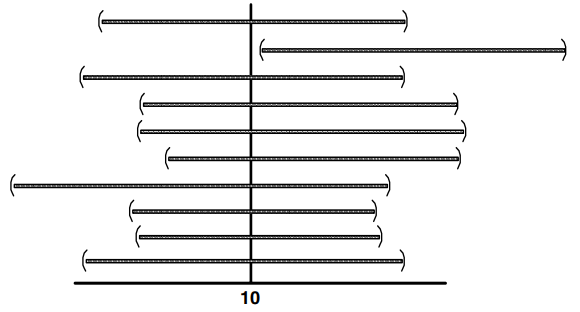
Figure 1: Sepuluh interval kepercayaan 90 persen data dengan nilai mean sebenarnya 10 (Helsel dan Hirsch, 2002)
Interval kepercayaan simetris pada rata-rata biasanya dihitung dengan asumsi data mengikuti distribusi normal. Jika tidak, distribusi rerata itu sendiri akan mendekati normal sepanjang ukuran sampel besar (katakanlah 50 pengamatan atau lebih besar). Interval kepercayaan dengan asumsi normalitas kemudian akan memasukkan mean sebenarnya (\(1-\alpha\))% dari waktu. Dalam contoh di atas, data dihasilkan dari distribusi normal, sehingga ukuran sampel kecil 12 tidak menjadi masalah. Namun ketika data memiliki kemencengan dan ukuran sampel di bawah 50 atau lebih, interval kepercayaan simetris tidak akan mengandung rata-rata (\(1-\alpha\))% sepanjang waktu. Dalam contoh di bawah ini, interval kepercayaan simetris secara salah dihitung untuk data yang miring (Gambar 2). Hasil (Gambar 3 dan Tabel 2) menunjukkan bahwa interval kepercayaan kehilangan nilai sebenarnya dari 1 lebih sering daripada yang seharusnya. Semakin besar skewness, semakin besar ukuran sampel harus sebelum interval kepercayaan simetris dapat diandalkan. Sebagai alternatif, interval kepercayaan asimetris dapat dihitung untuk situasi umum data yang memiliki kemencengan.
| No. | N | Mean | St.Dev | 90% Interval kepercayaan |
|---|---|---|---|---|
| 1 | 12 | 0,784 | 0,320 | \(^+\) 0,618 sampai 0,950 |
| 2 | 12 | 0,811 | 0,299 | \(^+\) 0,656 sampai 0,966 |
| 3 | 12 | 1,178 | 0,700 | 0,815 sampai 1,541 |
| 4 | 12 | 1,030 | 0,459 | 0,792 sampai 1,267 |
| 5 | 12 | 1,079 | 0,573 | 0,782 sampai 1,376 |
| 6 | 12 | 0,833 | 0,363 | 0,644 sampai 1,021 |
| 7 | 12 | 0,789 | 0,240 | \(^+\) 0,644 sampai 0,913 |
| 8 | 12 | 1,159 | 0,815 | 0,736 sampai 1,581 |
| 9 | 12 | 0,822 | 0,365 | \(^+\) 0,633 sampai 0,992 |
| 10 | 12 | 0,837 | 0,478 | 0,589 sampai 1,085 |
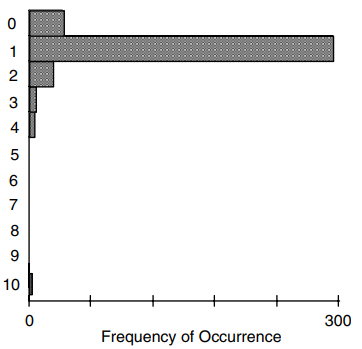
Figure 2: Histogram data dengan nilai mean populasi 1 dan simpangan baku populasi 0.75 (Helsel dan Hirsch, 2002)
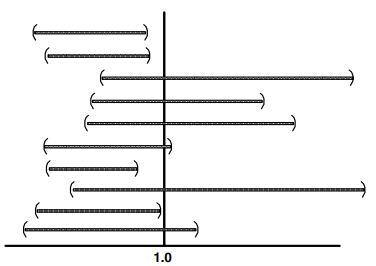
Figure 3: Sepuluh interval kepercayaan 90 persen data dengan nilai mean sebenarnya (Helsel dan Hirsch, 2002)
10.3 Interval Kepercayaan Median
Interval kepercayaan median populasi dapat dihitung tanpa perlu mengikuti asumsi distribusi tertentu. Sehingga nilai median dapat digunakan untuk memperkirakan nilai pusat data untuk distribusi data yang tidak berdistribusi normal.
10.3.1 Interval Estimasi Median Metode Nonparametrik
Interval estimasi nonparametrik untuk median populasi sebenarnya dihitung menggunakan distribusi binomial. Pertama, tingkat signifikansi yang diinginkan \(\alpha\) dinyatakan, error yang dapat diterima tidak termasuk median yang sebenarnya. Satu-setengah (\(\alpha/2\)) dari error ini digunakan untuk setiap akhir interval (Gambar 4). Tabel distribusi binomial memberikan nilai kritis bawah dan atas \(x'\) dan \(x\) pada setengah tingkat alfa yang diinginkan (\(\alpha/2\)). Nilai-nilai kritis ini ditransformasikan ke dalam rangking \(R_l\) dan \(R_u\) yang sesuai dengan titik data \(C_l\) dan \(C_u\) di ujung interval kepercayaan.
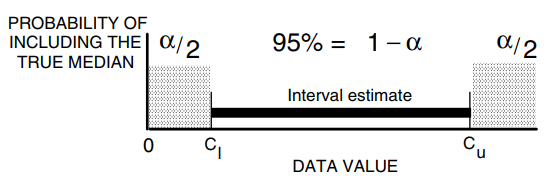
Figure 4: Probabilitas median populasi P50 pada dua sisi interval estimasi (Helsel dan Hirsch, 2002)
Untuk ukuran sampel kecil, tabel binomial dimasukkan pada kolom p = 0,5 (median) untuk menghitung interval kepercayaan pada median. Nilai kritis \(x'\) diperoleh dari tabel distribusi binomial yang sesuai dengan \(\alpha/2\), atau sedekat mungkin dengan \(\alpha/2\). Nilai kritis ini kemudian digunakan untuk menghitung peringkat \(R_u\) dan \(R_l\) yang sesuai dengan nilai data pada batas kepercayaan atas dan bawah untuk median. Batas-batas ini adalah titik data peringkat \(R_l\)th yang masuk dari setiap ujung daftar n observasi. Interval kepercayaan yang dihasilkan akan mencerminkan bentuk (menceng atau simetris) dari data asli.
\[\begin{equation} R_l=x'+1 \tag{2} \end{equation}\] \[\begin{equation} R_u=n-x'=x\ untuk\ x'\ dan\ x\ dari\ tabel\ dist.\ binomial \tag{3} \end{equation}\]Interval nonparametrik tidak selalu dapat secara tepat menghasilkan tingkat kepercayaan yang diinginkan ketika ukuran sampel kecil. Ini karena mereka terpisah, melompat dari satu nilai data ke yang berikutnya di ujung interval. Namun, tingkat kepercayaan yang dekat dengan yang diinginkan tersedia untuk semua kecuali ukuran sampel terkecil.
Untuk lebih memahaminya diberikan data 25 pengukuran konsentrasi arsenin di air tanah dalam ppb yang disajikan pada Tabel 3.
## Warning: package 'tibble' was built under R version 3.5.3| observasi | konsentrasi |
|---|---|
| 1 | 1.3 |
| 2 | 1.5 |
| 3 | 1.8 |
| 4 | 2.6 |
| 5 | 2.8 |
| 6 | 3.5 |
| 7 | 4.0 |
| 8 | 4.8 |
| 9 | 8.0 |
| 10 | 9.5 |
| 11 | 12.0 |
| 12 | 14.0 |
| 13 | 19.0 |
| 14 | 23.0 |
| 15 | 41.0 |
| 16 | 80.0 |
| 17 | 100.0 |
| 18 | 110.0 |
| 19 | 120.0 |
| 20 | 190.0 |
| 21 | 240.0 |
| 22 | 250.0 |
| 23 | 300.0 |
| 24 | 340.0 |
| 25 | 580.0 |
Visualisasi Tabel 3 ditunjukkan pada Gambar 5. Berdasarkan gambar tersebut terlihat bahwa data memiliki kemencengan yang positif sehingga penaksiran rata-rata populasi menggunakan nilai mean tidak dapat dilakukan.
## Warning: package 'ggplot2' was built under R version 3.5.3## Warning: package 'ggthemes' was built under R version 3.5.3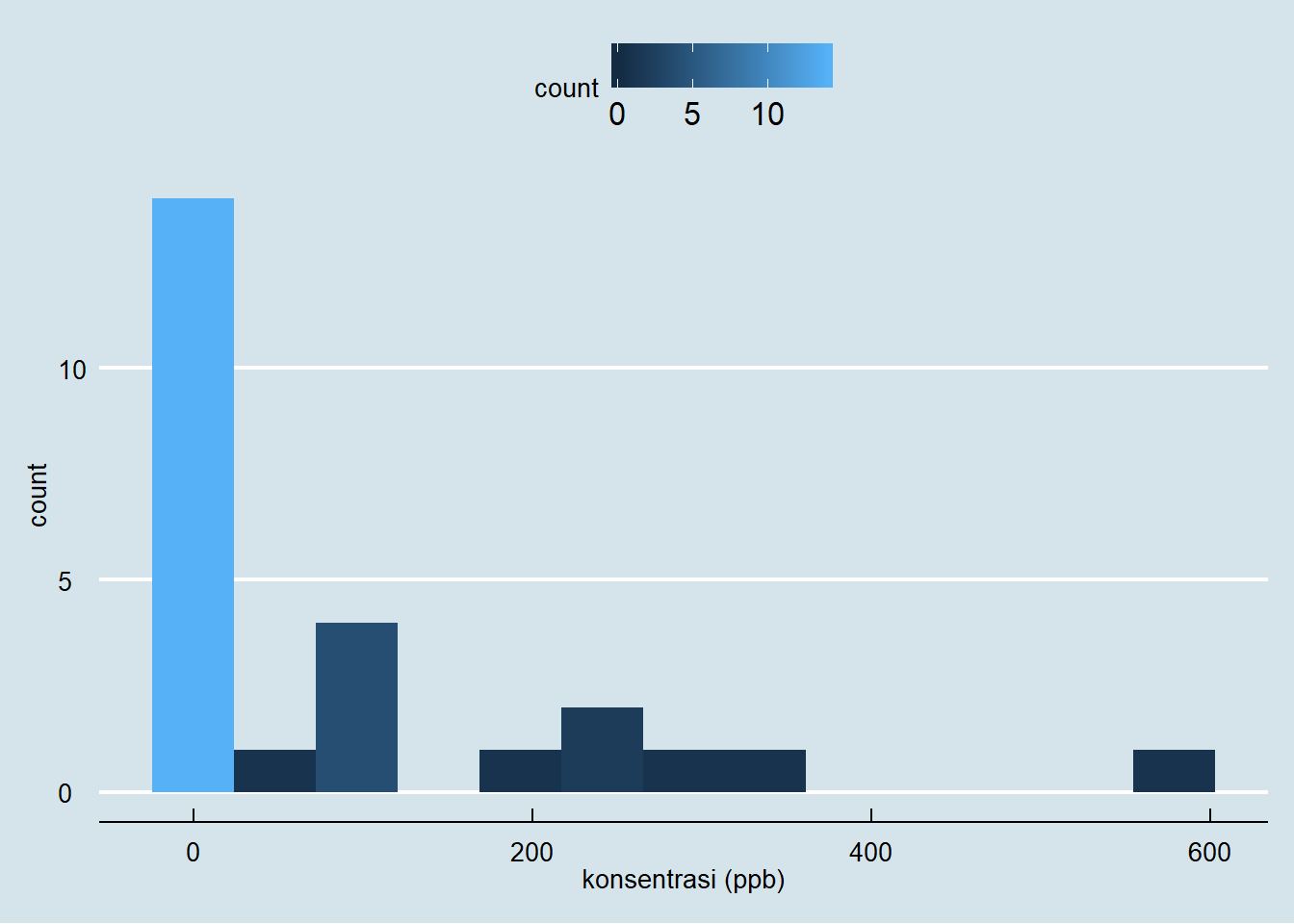
Figure 5: Distribusi konsentrasi arsenik dalam air tanah
Berdasarkan data pada Tabel 3, median konsentrasi arsenik \(\hat{C}_{0.5}\)=19 yang berada pada urutan data ke-13 dari data yang telah diurutkan dari yang terkecil ke yang terbesar. Untuk menentukan interval kepercayaan 95% median kosentrasi arsenik \(C_{0.5}\), nilai kritis berdasarkan nilai error mendekati \(\alpha/2\)=0,025 adalah \(x'\)=7. Untuk lebih memahaminya pembaca dapat mengunduh tabel distribusi binomial pada laman berikut. Nilai \(x'\)=7 diperoleh menggunakan Tabel distribusi binomial dengan \(n\)=25 dan \(p\)=0,5 yang ditampilkan pada Gambar 6 dengan nilai probabilitas sebesar 0,022 (mendekati 0,025) yang setara dengan area yang diarsir pada Gambar 4.
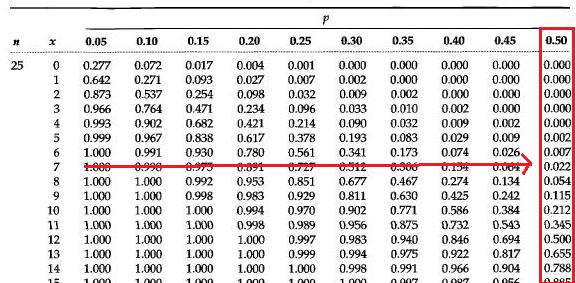
Figure 6: Lokasi probabilitas x berdasarkan tabel distribusi binomial
Berdasarkan Persamaan (2) dan Persamaan (3), rangking \(R_l\) pada observasi yang menyatakan batas kepercayaan bawah (lower confidence limit) adalah 8 (\(R_i\)=7+1) dan \(R_u\) yang menyatakan batas kepercayaan atas (upper confidence level) adalah 25-7=18. Berdasarkan nilai probabilitas \(x'\)=0,022, maka nilai alpha yang sesunggunya sebesar \(\alpha=2*0,022=0,044\). Nilai tersebut setara dengan tingkat kepercayaan \(1-0,044\) atau 95,6%. Nilai interval kepercayaan median antara observasi ke-8 dan 18 adalah \(C_l=4,8\le C_{0.5}\le110=C_u\ \ pada\ \alpha=0,044\). Nilai asimetrik disekitar \(\hat{C}_{0.5}\)=19 mencerminkan kemencengan pada data.
Jika pembaca ingin melakukan perhitungan pada R, pembaca harus membuat fungsi sebagai berikut:
med_npCI <- function(x,alpha){
# mengurutkan data
x_sort=sort(x)
# menghitung jumlah observasi
n=length(x)
# menghitung median data
med = median(x, na.rm=TRUE)
# loop untuk mencari nilai probabilitas terdekat
# dengan alpha
for(i in 1:n){
b = pbinom(i,n,0.5)
if(b>alpha/2){
break
}
}
# mengambil x'
x_i=i-1
# menghitung Rl dan Ru
rl=x_i+1
ru=n-x_i
# menghitung true confidence level
CL=1-2*(pbinom(x_i,n,0.5))
# menghitung Lower dan Upper CL
LCL=x_sort[rl]
UCL=x_sort[ru]
# menggabungkannya dalam satu data
data=data.frame("median"=med,
"True CL %"=CL*100,
"Lower CL"=LCL,
"Upper CL"=UCL)
return(data)
}Note:
- x: vektor numerik
- alpha: alpha level yang digunakan
Fungsi yang telah dibuat tersebut selanjutnya dapat pembaca gunakan saat akan menghitung interval kepercayaan median populasi menggunakan metode Nonparametrik. Berikut penerapannya menggunakan data pada Tabel 3 yang telah disimpan kedalam objek gwardat.
med_npCI(x=gwardat$konsentrasi, alpha=0.05)## median True.CL.. Lower.CL Upper.CL
## 1 19 95.67147 4.8 110Alternatif lain yang dapat digunakan untuk menghitung interval kepercayaan jika sampel cukup besar n>20 menggunakan metode Nonparametrik adalah dengan menggunakan pendekatan tabel distribusi normal untuk memperkirakan distribusi binomial. Dengan menggunakan pendekatan ini, hanya sebagian kecil tabel distribusi binomial (n=20) yang diperlukan untuk melakukannya. Nilai kritis \(z_{\alpha/2}\) dari tabel distribusi normal menentukan rangking atas dan bawah observasi yang menyatakan awal dan akhir nilai interval kepercayaan yang dinyatakan pada Persamaan (4) dan Persamaan (5). Pembulatan diperlukan dalam proses ini sebab nilai ranking harus berupa integer.
\[\begin{equation} R_l=\frac{n-z_{\frac{\alpha}{2}}\cdot\sqrt{n}}{2} \tag{4} \end{equation}\] \[\begin{equation} R_l=\frac{n-z_{\frac{\alpha}{2}}\cdot\sqrt{n}}{2}+1 \tag{5} \end{equation}\]Menggunakan contoh data pada Tabel 3, dengan 95% interval kepercayaan (\(z_{\alpha/2}\)=1,96) median dapat dihitung seperti berikut:
\[ R_l=\frac{25-1,96\cdot\sqrt{25}}{2}=7,6 \]
\[ R_l=\frac{25+1,96\cdot\sqrt{25}}{2}+1=18,4 \]
Berdasarkan hasil perhitungan diperoleh rangking bawah adalah data ke-8 dan rangking atas adalah 18. Kedua data dibulatkan berdasarkan integer terdekat. Nilai interval kepercayaan median yang diperoleh sama dengan metode sebelumnya sebab rangking batas bawah dan atasnya yang seragam.
Jika pembaca ingin menggunakan R, maka fungsi yang sebelumya telah kita buat dapat dimodifikasi seperti berikut:
med_norCI <- function(x, alpha){
# mengurutkan data dari yang terkecil
x_sort=sort(x)
# menghitung jumlah observasi
n = length(x)
# menghitung median data
med = median(x, na.rm=TRUE)
# menghitung Rl dan Ru
rl=round((n-abs(qnorm(alpha/2))*sqrt(n))/2,0)
ru=round(((n+abs(qnorm(alpha/2))*sqrt(n))/2)+1,0)
# menghitung Lower dan Upper CL
LCL=x_sort[rl]
UCL=x_sort[ru]
# menggabungkannya dalam satu data
data=data.frame("median"=med,
"Lower CL"=LCL,
"Upper CL"=UCL)
return(data)
}Fungsi med_norCI() sama dengan fungsi med_npCI(). Perbedaannya terletak pada penggunaan distribusi normal pada proses penentuan titik kritisnya.
Dengan menggunakan fungsi med_norCI(), rentang kepercayaan median dapat dihitung seperti berikut:
Note:
- x: vektor numerik
- alpha: alpha level yang digunakan
med_norCI(x=gwardat$konsentrasi, alpha=0.05)## median Lower.CL Upper.CL
## 1 19 4.8 110Jika kita tidak ingin menggunakan vektor dalam fungsi, kita dapat juga menggunakan data frame sebagai inputnya. Kelebihannya adalah kita dapat menghitung rentang kepercayaan seluruh kolom dalam satu kali proses. Hal ini tentunya akan menghemat waktu yang digunakan. Berikut adalah contoh sintaks fungsi untuk menghitung interval kepercayaan median menggunakan distribusi normal dengan metode nonparametrik yang digunakan:
med_norCI <- function(df, alpha){
# membuat matrik untuk menyimpan
# hasil loop
med = rep(NA, ncol(df))
LCL = rep(NA, ncol(df))
UCL = rep(NA, ncol(df))
var = rep(NA, ncol(df))
# looping
for(i in 1:ncol(df)){
# mengurutkan data
x_sort = sort(df[, i])
# mengambil nama kolom dataset
var[i] = colnames(df[i])
# menghitung jumlah observasi
n = length(x_sort)
# menghitung median data
med[i] = median(x_sort, na.rm=TRUE)
# menghitung Lower dan Upper CL
LCL[i]=x_sort[(round((n-abs(qnorm(alpha/2))*sqrt(n))/2,0))]
UCL[i]=x_sort[(round(((n+abs(qnorm(alpha/2))*sqrt(n))/2)+1,0))]
}
# menggabungkannya dalam satu data
data=data.frame("variabel"=var,
"median"=med,
"Lower CL"=LCL,
"Upper CL"=UCL)
return(data)
}Note:
- df: data frame
- alpha: alpha level yang digunakan
Fungsi tersebut dapat menghitung sekaligus Interval kepercayaan median dengan metode nonparametrik. Pembaca dapat mencobanya dengan menggunakan dataset yang pembaca miliki. Pembaca dapat mengabaikan peringatan yang muncul dan berfokus pada hasil yang diperoleh. Sebagai contoh jalankan fungsi tersebut menggunakan dataset airquality berikut:
med_norCI(df=airquality, alpha=0.05)10.3.2 Metode Parametrik Interval Estimasi Median
Telah dijelaskan pada chapter 6 bahwa rata-rata geometrik merupakan merupakan nilai rata-rata yang digunakan untuk mengestimasi median sampel untuk data yang memiliki kemencengan dengan transformasi yang digunakan agar data simetris adalah transformasi logaritmik \(y=\ln(x)\). Pada metode ini data diasumsikan memiliki distribusi lognormal (kemencengan positif). Rerata dan interval geometris akan lebih efisien (interval lebih pendek) dari median dan interval kepercayaannya ketika data benar-benar lognormal. Median sampel dan intervalnya lebih tepat dan lebih efisien jika logaritma data masih menunjukkan kemencengan dan/atau outlier. Estimasi media menggunakan metode parametrik dituliskan kedalam Persamaan (6) dan Persamaan (7).
\[\begin{equation} GM_x=\exp\left(\overline{y}\right) \tag{6} \end{equation}\]dimana \(y=\ln(x)\) dan \(\overline{y}\)=mean sampel \(y\).
\[\begin{equation} \exp\left(\overline{y}-t_{\left(\frac{\alpha}{2},n-1\right)}\sqrt{\frac{s_y^2}{n}}\right)\le GM_x\le\exp\left(\overline{y}+t_{\left(\frac{\alpha}{2},n-1\right)}\sqrt{\frac{s_y^2}{n}}\right) \tag{7} \end{equation}\]dimana \(s_{y}^2\)= varians sampel y pada unit log natural.
Pada Tabel 3, untuk menghitung interval keyakinan median menggunakan pendekatan mean geometrik \(GM_x\) kita perlu mentransformasi datanya terlebih dahulu sehingga menjadi bentuk natural log. hasil transformasi disajikan pada Tabel 4.
| observasi | konsentrasi |
|---|---|
| 1 | 0.2623643 |
| 2 | 0.4054651 |
| 3 | 0.5877867 |
| 4 | 0.9555114 |
| 5 | 1.0296194 |
| 6 | 1.2527630 |
| 7 | 1.3862944 |
| 8 | 1.5686159 |
| 9 | 2.0794415 |
| 10 | 2.2512918 |
| 11 | 2.4849066 |
| 12 | 2.6390573 |
| 13 | 2.9444390 |
| 14 | 3.1354942 |
| 15 | 3.7135721 |
| 16 | 4.3820266 |
| 17 | 4.6051702 |
| 18 | 4.7004804 |
| 19 | 4.7874917 |
| 20 | 5.2470241 |
| 21 | 5.4806389 |
| 22 | 5.5214609 |
| 23 | 5.7037825 |
| 24 | 5.8289456 |
| 25 | 6.3630281 |
visualisasi distribusi yang baru disajikan pada Gambar 7.
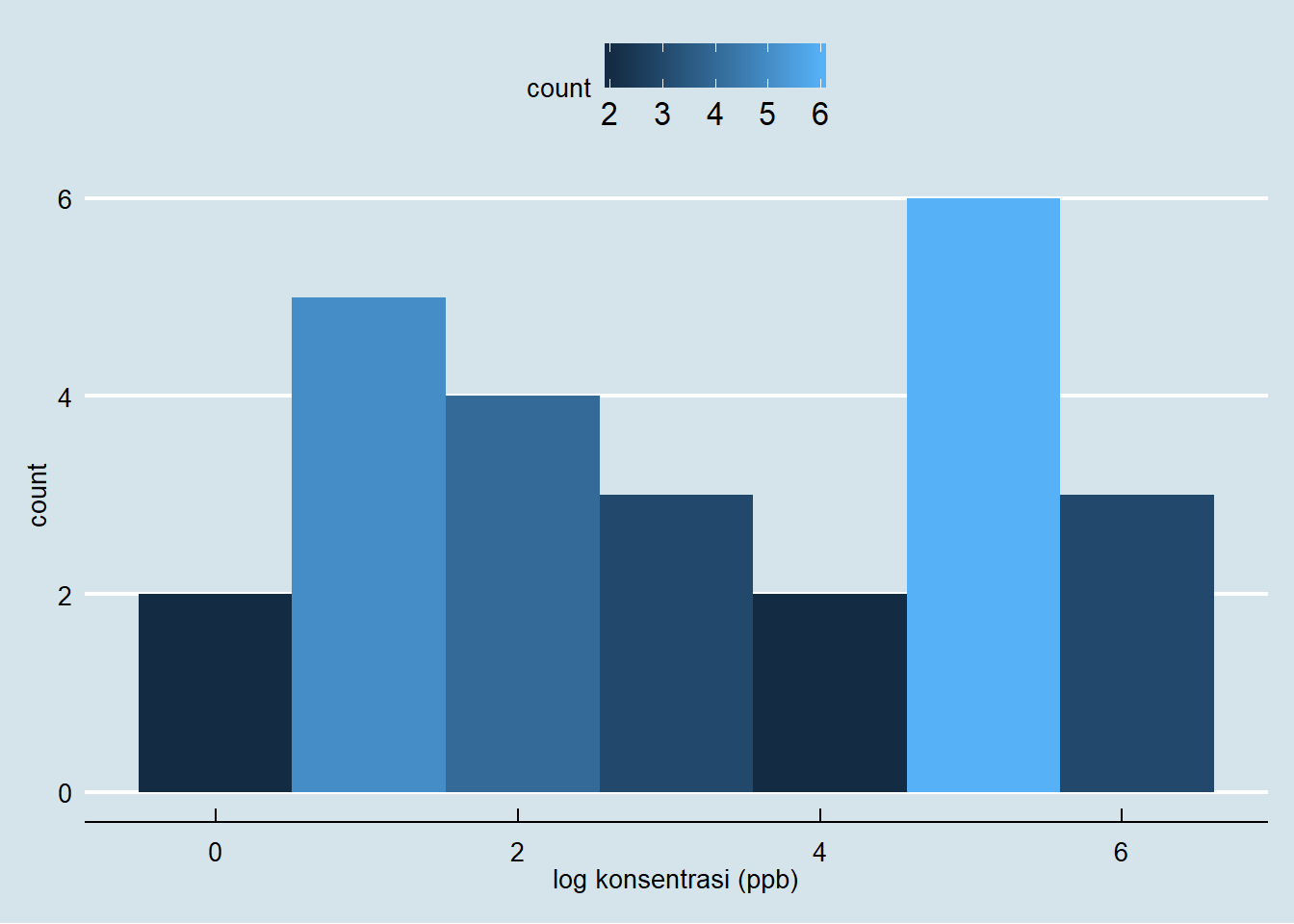
Figure 7: Distribusi logaritmik konsentrasi arsenik dalam air tanah
Nilai mean dari data tersebut adalah 3,17 dengan simpangan baku sebesar 1,96. Berdasarkan Gambar 7, kita telah memperoleh distribusi yang simetris.
Dengan menggunakan Persamaan (6) dan Persamaan (7) selanjutnya dapat dihitung interval kepercayaannya dengan derajat kepercayaan 95%.
\[ GM_x=\exp\left(3,17\right)=23,8 \]
\[ \exp\left(3.17-2,064\cdot\sqrt{\frac{1.96^2}{25}}\right)\le GM_x\le\exp\left(3.17-2,064\cdot\sqrt{\frac{1.96^2}{25}}\right) \]
\[ \exp\left(2,36\right)\le GM_x\le\exp\left(3,98\right) \]
\[ 10,6\le GM_x\le53,5 \]
Dengan menggunakan R dapat dikerjakan menggunakan fungsi sebagai berikut:
med_gm <- function(x, alpha){
x = log(x)
# rata-rata geometrik
gm = exp(mean(x, na.rm=TRUE))
# menghitung derajat kebebasan
df = length(x)-1
# menghitung batas bawah dan atas
LCL = exp(mean(x, na.rm=TRUE)-qt(1-alpha/2,df)*sqrt(var(x, na.rm=TRUE)/length(x)))
UCL = exp(mean(x, na.rm=TRUE)+qt(1-alpha/2,df)*sqrt(var(x, na.rm=TRUE)/length(x)))
# menggabungkan hasil
data=data.frame("GM"=gm,
"Lower CL"=LCL,
"Upper CL"=UCL)
return(data)
}Note:
- x: vektor numerik
- alpha: alpha level yang digunakan
med_gm(x=gwardat$konsentrasi, alpha=0.05)## GM Lower.CL Upper.CL
## 1 23.87106 10.63118 53.59966Fungsi med_gm() dapat dilakukan sejumlah modifikasi seperti penggunaan data frame sebagai input serta proses transformasi yang dilakukan didalam fungsi yang ada sekaligus. Berikut adalah contoh fungsi yang digunakan untuk input berupa data frame dan proses transformasi termasuk didalamnya:
med_gm <- function(df, alpha){
# membuat vektor untuk menyimpan hasil loop
var = rep(NA, ncol(df))
gm = rep(NA, ncol(df))
LCL = rep(NA, ncol(df))
UCL = rep(NA, ncol(df))
# looping
for(i in 1:ncol(df)){
# mengambil nama kolom
var[i] = colnames(df[i])
# transformasi variabel (logaritmik)
x = log(df[,i])
# rata-rata geometrik
gm[i] = exp(mean(x, na.rm=TRUE))
# menghitung derajat kebebasan
d = length(x)-1
# menghitung batas bawah dan atas
LCL[i] = exp(mean(x, na.rm=TRUE)-qt(1-alpha/2,d)*sqrt(var(x, na.rm=TRUE)/length(x)))
UCL[i] = exp(mean(x, na.rm=TRUE)+qt(1-alpha/2,d)*sqrt(var(x,na.rm=TRUE)/length(x)))
}
# menggabungkan hasil
data=data.frame("Variabel"=var,
"GM"=gm,
"Lower CL"=LCL,
"Upper CL"=UCL)
return(data)
}Note:
- df: data frame
- alpha: alpha level yang digunakan
Untuk menguji fungsi tersebut jalankan fungsi tersebut menggunakan dataset yang pembaca miliki. Dalam contoh ini ak diberikan contoh penerapannya menggunakan dataset airquality. Jalankan fungsi berikut untuk memperoleh hasilnya.
med_gm(airquality, 0.05)Pembaca perlu berhati-hati dalam menentukan apakah akan menggunakan metode Nonparametrik atau parametrik. Jika data berditribusi lognormal kita dapat menggunakan metode parametrik.
10.4 Interval Kepercayaan Mean
Estimasi interval juga dapat dihitung untuk mean populasi sebenarnya \(\mu\). Hal ini sangat sesuai jika pusat data menjadi fokus dalam analisa statistik. Interval simetris di sekitar sampel rata-rata X paling sering dihitung. Untuk ukuran sampel besar, interval simetris secara memadai menggambarkan variasi rata-rata, terlepas dari bentuk distribusi data. Ini karena distribusi rata-rata sampel akan mendekati dengan distribusi normal ketika ukuran sampel semakin besar, meskipun data mungkin tidak terdistribusi secara normal. Untuk ukuran sampel yang lebih kecil, rata-rata tidak akan didistribusikan secara normal kecuali jika data itu sendiri terdistribusi secara normal. Ketika data meningkat kemencengannya, lebih banyak data diperlukan sebelum distribusi rata-rata dapat didekati secara memadai oleh distribusi normal. Untuk distribusi yang sangat miring atau data yang mengandung outlier, mungkin diperlukan lebih dari 100 pengamatan sebelum nilai rata-rata tidak akan terpengaruh oleh nilai terbesar untuk mengasumsikan bahwa distribusinya akan simetris.
10.4.1 Interval Kepercayaan Mean Untuk Distribusi Yang Simetris
Interval kepercayaan mean untuk distribusi simetris dihitung menggunakan tabel distribusi student’s t yang tersedia dalam buku teks statistik dan perangkat lunak. Tabel ini dimasukkan untuk menemukan nilai kritis untuk t pada setengah tingkat alfa yang diinginkan. Pada buku lain sering dijelaskan bahwa distribusi t hanya digunakan untuk sampel kecil (beberapa menyebutkan n<30), sedangkan untuk distribusi besar digunakan distribusi normal. Penggunaan distribusi normal jarang digunakan dalam prakiraan. Hal ini disebabkan karena pada proses perhitungan diperlukan nilai simpangan baku \(\sigma\). Pada kenyataannya pada pengukuran dilapangan kita sering sekalin melakukan estimasi terhadap simpangan baku melalui sampel \(s\) karena kita tidak mengetahui nilai simpangan baku populasinya sehingga pada buku ini akan digali lebih jauh metode estimasi interval menggunakan persamaan distribusi t.
Lebar interval kepercayaan adalah fungsi dari nilai-nilai kritis dari tabel distribusi t, simpangan baku data, dan ukuran sampel. Ketika data memiliki kemecengan atau mengandung outlier, asumsi di balik interval t dan distribusi normal tidak berlaku. Interval simetris yang dihasilkan akan sangat luas sehingga sebagian besar pengamatan akan dimasukkan di dalamnya. Ini juga dapat mencapai di bawah nol di ujung bawah. Titik akhir negatif dari interval kepercayaan untuk data yang tidak dapat menjadi negatif adalah sinyal yang jelas bahwa asumsi interval kepercayaan simetris tidak diperlukan. Untuk data tersebut, dengan asumsi distribusi lognormal seperti yang dijelaskan dalam sub chapter sebelumnya (interval kepercayaan median) akan lebih tepat. Interval kepercayaan dihitung menggunakan Persamaan (8).
\[\begin{equation} \overline{x}-t_{\left(\frac{\alpha}{2},n-1\right)}\cdot\sqrt{\frac{s^2}{n}}\le\mu\le\overline{x}+t_{\left(\frac{\alpha}{2},n-1\right)}\cdot\sqrt{\frac{s^2}{n}} \tag{8} \end{equation}\]Untuk lebih memahami cara penerapannya, kita akan menggunakan kembali data pada Tabel 4. Langkah pertama yang perlu dilakukan adalah menghitung mean sampel \(\overline{x}\) dan simpangan baku sampel \(s\). Berdasarkan hasil perhitungan diperoleh nilai \(\overline{x}\) =98.352 dan \(s\) = 144.685. Dengan meggunakan Persamaan (8), interval estimasi mean dengan tingkat kepercayaan 95% dapat dihitung sebagai berikut:
\[ 3,17\ -\ t_{\left(0.25,24\right)}\cdot\sqrt{\frac{1,96^2}{25}}\le\mu\le3,17\ -\ t_{\left(0.25,24\right)}\cdot\sqrt{\frac{1,96^2}{25}} \]
\[ 2,36\le\mu\le3,98 \]
Berdasarkan hasil yang diperoleh terdapat 95% peluang nilai mean populasi \(\mu\) terletak pada interval 2,36 sampai 3,98. Perlu diingat bahwa metode parametrik sangat sensitif dengan adanya outlier sehingga jika pembaca ingin menggunakannya pastikan terlebih dahulu tidak ada outlier pada data dengan cara melakukan visualisasi data.
Pada R kita dapat menggunakan fungsi stat.desc() untuk menhitung statistika deskriptif serta interval kepercayaan mean-nya. Berikut adalah sintaks yang digunakan:
# memuat paket
library(pastecs)## Warning: package 'pastecs' was built under R version 3.5.3# ringkasan data
r=stat.desc(gwardat2$konsentrasi)
r## nbr.val nbr.null nbr.na min max
## 25.0000000 0.0000000 0.0000000 0.2623643 6.3630281
## range sum median mean SE.mean
## 6.1006638 79.3166718 2.9444390 3.1726669 0.3919164
## CI.mean.0.95 var std.dev coef.var
## 0.8088758 3.8399625 1.9595822 0.6176451# batas bawah (LCL)
mean(gwardat2$konsentrasi)-r[[11]]## [1] 2.363791# batas atas (UCL)
mean(gwardat2$konsentrasi)+r[[11]]## [1] 3.981543Selain itu , kita juga dapat menghitung interval kepercayaan mean menggunakan fungsi t.test(). Fungsi ini pada dasarnya dilakukan untuk melakukan uji hipotesis terhadap satu rata-rata. Untuk lebih tahu mengenai fungsi tersebut jalankan sintaks bantuan berikut:
?t.testUntuk menghitung interval kepercayaan mean jalankan sintaks berikut:
t.test(gwardat$konsentrasi, conf.level= 0.95) ##
## One Sample t-test
##
## data: gwardat$konsentrasi
## t = 3.3988, df = 24, p-value = 0.002364
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
## 38.62894 158.07506
## sample estimates:
## mean of x
## 98.35210.4.2 Interval Kepercayaan Mean Untuk Distribusi Yang Asimetris
Mean dan interval kepercayaan dapat dihitung dengan mengasumsikan distribusi data mengikuti distribusi logaritmik \(y=\ln{(x)}\). Metode ini berguna untuk jenis data yang memiliki bentuk distribusi data yang memiliki kemencengan positif (perlu transformasi logaritmik agar simetris).Metode ini memberikan perkiraan rata-rata yang lebih dapat diandalkan (varians lebih rendah) daripada perhitungan rata-rata sampel biasa tanpa transformasi log.
Untuk memperkirakan rata-rata populasi \(\mu_x\) dalam unit aslinya, anggap datanya berdistribusi normal. Satu-setengah varians logaritma ditambahkan ke \(\overline{y}\) (rata-rata log) sebelum eksponensial. Karena varians sampel \(s^2_y\) hanya perkiraan varians sebenarnya dari logaritma, estimasi sampel rata-rata akan menjadi bias. Namun, untuk sampel dengan \(s^2_y\) kecil dan ukuran sampel besar bias dapat diabaikan. Interval kepercayaan dapat dituliskan berdasarkan Persamaan (9).
\[\begin{equation} \mu_x=\exp\left(\overline{y}+0,5\cdot s_y^2\right) \tag{9} \end{equation}\]dimana \(y=\ln{(x)}\), \(\overline{y}\)= mean sampel dan \(s^2_y\)= varians sampel y dalam unit log natural.
Interval kepercayaan sekitar \(\mu_x\) bukan estimasi interval yang dihitung untuk rata-rata geometri dalam Persamaan (7). Interval kepercayaan tidak dapat dihitung hanya dengan mengekspansi interval sekitar \(\overline{y}\). Interval kepercayaan yang tepat dalam satuan asli untuk rata-rata data lognormal dapat dihitung. Untuk lebih jelasnya pembaca dapat melihatnya pada situs http://jse.amstat.org/v13n1/olsson.html.
Metode Cox dapat digunakan untuk menghitung interval keyakinan dengan nilai estimasi rata-rata menggunakan Persamaan (9). Persamaan yang digunakan dapat dituliskan sebagai berikut (Persamaan (10)).
\[\begin{equation} \ln\left(\mu_x\right)=\overline{Y}+\frac{s_y^2}{2}\pm z_{\left(\frac{\alpha}{2}\right)}\sqrt{\frac{s_y^2}{n}+\frac{s_y^4}{2\left(n-1\right)}} \tag{10} \end{equation}\]Persamaan (10) dapat dimodifikasi dengan menggunakan distribusi t dibanding menggunakan distribusi normal. Penggunaan distribusi t akan memperbaiki kelemahan penggunaan distribusi normal pada sampel yang berukuran kecil.
Data Tabel 3 dapat kita gunakan untuk menghitung rata-rata menggunakan Persamaan (10). Hal ini disebabkan karena data yang ada memiliki kemencengan positif sehingga dapat dianggap bahwa transformasi logaritmik dapat membentuk distribusi ini menjadi lebih simetris.
Berdasarkan hasil perhitungan diperoleh nilai \(\overline{Y}\) =3.173 dan \(s^2_y\) = 1.96. Sehingga nilai interval selanjutnya dapat dihitung menggunakan Persamaan (10) dengan interval keyakinan 95%.
\[ \ln\left(\mu_x\right)=3,17+\frac{1,96^2}{2}\pm1,96\sqrt{\frac{1,96^2}{25}+\frac{1,96^4}{2\left(25-1\right)}} \]
\[ \ln\left(\mu_x\right)=5,10\pm1,33 \]
Sehingga
\[ \exp\left(5,10-1,33\right)\le\mu_x\le\exp\left(5,10+1,33\right) \]
\[ 43,38\le\mu_x\le620,17 \]
Nilai interval yang dihasilkan sangat panjang sehingga nilai rata-rata yang dihasilkan tidak dapat diandalkan untuk memperkirankan lokasi nilai mean populasi.
Pada contoh berikut akan disajikan sintaks untuk menghitung interval kepercayaan mean data pada Tabel 3 berdasarkan Persamaan (10) dan sitribusi yang digunakan adalah distribusi t. Pembaca dapat memodifikasi sintaks berikut jika ingin menggunakan distribusi normal.
mean_asci<-function(x,alpha){
m=mean(x, na.rm=TRUE)
# mean data hasil transformasi logaritmik
ave = mean(log(x), na.rm=TRUE)
# simpangan baku data hasil transformasi
sd = sd(log(x), na.rm=TRUE)
# jumlah observasi
n = length(x)
# derajat kebebasa
df = n-1
# interval keyakinan satu sisi
re = 1-(alpha/2)
# CI menggunakan distribusi t
LCL = exp(ave+(0.5*sd^2)-qt(re,df)*sqrt(((sd^2)/n)+((sd^4)/(2*df))))
UCL = exp(ave+(0.5*sd^2)+qt(re,df)*sqrt(((sd^2)/n)+((sd^4)/(2*df))))
# menggabungkan hasil
data = data.frame("Mean"=m,
"Lower CL"=LCL,
"Upper CL"=UCL)
return(data)
}Note:
- x: vektor numerik
- alpha: alpha level yang digunakan
mean_asci(x=gwardat$konsentrasi, alpha=0.05)## Mean Lower.CL Upper.CL
## 1 98.352 40.11052 660.9363Jika pembaca ingin menggunakan data frame sebagai input yang digunakan selain vektor, fungsi tersebut dapat dimodifikasi seperti berikut:
mean_asci<-function(df,alpha){
# membuat vektor untuk menyimpan hasil loop
var = rep(NA, ncol(df))
m = rep(NA, ncol(df))
LCL = rep(NA, ncol(df))
UCL = rep(NA, ncol(df))
# looping
for(i in 1:ncol(df)){
# mengambil nama kolom
var[i] = colnames(df[i])
# menghitung mean data
m[i]=mean(df[,i], na.rm=TRUE)
# mean data hasil transformasi logaritmik
ave = mean(log(df[,i]), na.rm=TRUE)
# simpangan baku data hasil transformasi
sd = sd(log(df[,i]), na.rm=TRUE)
# jumlah observasi
n = length(df[,i])
# derajat kebebasa
d = n-1
# interval keyakinan satu sisi
re = 1-(alpha/2)
# CI menggunakan distribusi t
LCL[i] = exp(ave+(0.5*sd^2)-qt(re,d)*sqrt(((sd^2)/n)+((sd^4)/(2*d))))
UCL[i] = exp(ave+(0.5*sd^2)+qt(re,d)*sqrt(((sd^2)/n)+((sd^4)/(2*d))))
}
# menggabungkan hasil
data = data.frame("Variabel"=var,
"Mean"=m,
"Lower CL"=LCL,
"Upper CL"=UCL)
return(data)
}Note:
- df: data frame
- alpha: alpha level yang digunakan
Untuk menguji fungsi tersebut, pembaca dapat memasukkan data frame yang pembaca miliki kedalam persamaan tersebut. Berikut adalah contoh sintaks yang digunakan untuk menghitung interval kepercayaan mean pada dataset airquality. Pembaca dapat menjalankannya pada komputer pembaca.
mean_asci(airquality, 0.05)10.5 Interval Prediksi Nonparametrik
Pertanyaan yang sering diajukan adalah apakah satu pengamatan baru kemungkinan berasal dari distribusi yang sama dengan data yang dikumpulkan sebelumnya, atau sebagai alternatif dari distribusi yang berbeda. Pertanyaan dapat dievaluasi dengan menentukan apakah pengamatan baru di luar interval prediksi yang dihitung dari data yang ada. Interval prediksi mengandung \(100\cdot\left(1-\alpha\right)\) persen dari distribusi data, sementara \(100\cdot\alpha\) persen berada di luar interval. Jika pengamatan baru datang dari distribusi yang sama dengan data yang diukur sebelumnya, ada kemungkinan \(100\cdot\alpha\) persen bahwa pengamatan baru tersebut akan berada di luar interval prediksi. Karena pengamatan baru tersebut berada di luar interval tidak “membuktikan” pengamatan baru itu berbeda, hanya saja sepertinya begitu. Seberapa besar kemungkinan ini tergantung pada pilihan \(\alpha\) yang ditentukan oleh peneliti.
Interval prediksi dihitung dengan tujuan yang berbeda dari interval kepercayaan. Interval prediksi terkait dengan nilai data individu yang berlawanan dengan ringkasan statistik seperti nilai mean. Interval prediksi lebih luas daripada interval kepercayaan, karena pengamatan individu lebih bervariasi daripada ringkasan statistik yang dihitung dari beberapa pengamatan. Tidak seperti interval kepercayaan, interval prediksi memperhitungkan variabilitas titik data tunggal di sekitar median atau rata-rata, di samping kesalahan dalam memperkirakan pusat distribusi. Ketika mean \(\pm\) 2 simpangan baku secara keliru digunakan untuk memperkirakan lebar interval prediksi, data baru dinyatakan berasal dari populasi yang berbeda lebih sering daripada yang seharusnya.
10.5.1 Interval Prediksi Nonparametrik Dua Sisi
Interval prediksi tingkat kepercayaan nonparametrik \(\alpha\) secara sederhana dinyatakan sebagai interval antara persentil distribusi \(\alpha/2\) dan \(1-\left(\frac{\alpha}{2}\right)\) (Gambar 8). Interval ini mengandung \(100\cdot\left(1-\alpha\right)\) data, sedangkan \(100\cdot\alpha\) persen berada di luar interval. Oleh karena itu jika titik data tambahan baru berasal dari distribusi yang sama dengan data yang diukur sebelumnya, ada kemungkinan \(100\cdot\alpha\) persen bahwa itu akan berada di luar interval prediksi. Interval akan mencerminkan bentuk data yang dikembangkannya, dan tidak ada asumsi tentang bentuk bentuk yang perlu dibuat. Interval prediksi nonparametrik dua sisi dinyatakan berdasarkan Persamaan (11).
\[\begin{equation} PI_{np}=X_{\frac{\alpha}{2}\cdot\left(n+1\right)}\ sampai\ dengan\ X_{\left[1-\left(\frac{\alpha}{2}\right)\right]\cdot\left(n+1\right)} \tag{11} \end{equation}\]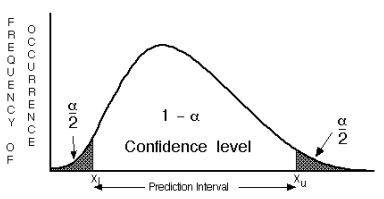
Figure 8: Prediksi interval dua sisi (Helsel dan Hirsch, 2002)
Kita akan kembali menggunakan data pada Tabel 3. Dengan menggunakan tingkat kepercayaan 90% kita diminta untuk menentukan interval prediksi dari konsentrasi arsenik pada data tersebut tanpa mengasumsikan distribusi dari data.
Untuk melakukannya kita perlu menentukan observasi ke-2,5 dan 97,5 (berdasarkan nilai \(\alpha/2\)) dengan rangking observasi berdasarkan Persamaan (11) adalah \((0,05*26)\) atau rangking observasi antara observasi 1 (\(R_1\)) dan 2 (\(R_2\)) dan \((0,95*26)\) rangking observasi antara observasi 24 (\(R_{24}\)) dan 25 (\(R_{25}\)). Dengan menggunakan interpolasi linier pada observasi ke-1, 2 , 24 dan 25, interval prediksi yang diperoleh adalah sebagai berikut:
\[ X_1+\left(\frac{R_{\left(0.05\cdot26\right)}-R_1}{R_2-R_1}\right)\cdot\left(X_2-X_1\right)\ sampai\ dengan\ X_{24}+\left(\frac{R_{\left(0.95\cdot26\right)}-R_{24}}{R_{25}-R_{24}}\right)\cdot\left(X_{25}-X_4\right) \]
\[ 1,3+\left(\frac{1,3-1}{2-1}\right)\cdot\left(1,5-1,3\right)\ sampai\ dengan\ 340+\left(\frac{24,5-24}{25-24}\right)\cdot\left(580-340\right) \]
\[ 1,4\ sampai\ dengan\ 508\ ppb \]
Observasi baru diluar rentang tersebut akan dianggap berasal dari distribusi yang berbeda dengan tingkat error sebesar 10% (\(\alpha\)=10%).
Dengan menggunakan R pembaca depat menghitung interval prediksi menggunakan fungsi berikut:
PInp <- function(x, alpha){
# mengurutkan data
x_sort = sort(x)
# jumlah observasi
n = length(x)
# menghitung alpha masing-masing sisi
err <- alpha/2
# menentukan rangkin observasi sesuai alpha
rl = err*(n+1)
ru = (1-err)*(n+1)
# menentukan observasi untuk interpolasi linier
rl_1= ceiling(rl) # bulatkan ke bawah
rl_2= floor(rl) # bulatkan ke atas
ru_1= ceiling(ru)
ru_2= floor(ru)
# menentukan interval prediksi
LPI = round(x_sort[rl_1]+((rl-rl_1)/(rl_2-rl_1))*(x_sort[rl_2]-x_sort[rl_1]),1)
UPI = round(x_sort[ru_1]+((ru-ru_1)/(ru_2-ru_1))*(x_sort[ru_2]-x[ru_1]),1)
# menggabungkan hasil
data = data.frame("Lower PI"=LPI,
"Upper PI"=UPI)
return(data)
}Note:
- x: vektor numerik
- alpha: alpha level yang digunakan
PInp(x=gwardat$konsentrasi, alpha=0.1)## Lower.PI Upper.PI
## 1 1.4 50810.5.2 Interval Prediksi Nonparametrik Satu Sisi
Interval prediksi satu sisi digunakan jika kita ingin mengecek apakah pengamatan baru lebih besar dari data yang ada, atau lebih kecil dari data yang ada, tetapi tidak keduanya. Keputusan untuk menggunakan interval satu sisi harus didasarkan sepenuhnya pada pertanyaan yang menarik. Seharusnya tidak ditentukan setelah melihat data dan memutuskan bahwa pengamatan baru cenderung hanya lebih besar, atau hanya lebih kecil, daripada informasi yang ada. Interval satu sisi menggunakan \(\alpha\) dibanding \(\alpha/2\) sebagai nilai error, menempatkan semua error di satu sisi interval (Gambar 9). Interval prediksi dituliskan berdasarkan Persamaan (12).
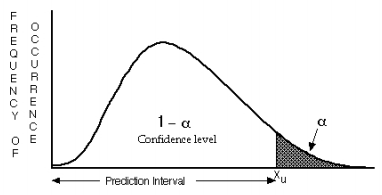
Figure 9: Prediksi interval satu sisi (Helsel dan Hirsch, 2002)
Untuk memahami penerapannya, misalkan kita memiliki nilai arsenik baru dengan konsentrasi 355 ppb. Kita perlu menentukan apakah nilai tersebut lebih besar dari sebagian besar data yang ada.
Dengan menggunakan Persamaan (12) dan \(\alpha\)=0,1 atau tingkat kepercayaan 90%, interval prediksi satu sisi atau data teratas dari persentil ke-90 dari data yang ada adalah \(X_{0,9}*26=X_{23,4}\). Dengan menggunakan interpolasi linier pada observasi data dengan rangking ke-23 (\(R_{23}\)) dan 24 (\(R_{23}\)) diperoleh:
\[ X_{23}+0,4\cdot\left(X_{24}-X_{23}\right)=300+0,4\cdot40=316\ ppb \]
Berdasarkan data yang diperoleh diketahui bahwa batas atas dari interval prediksi adalah 316<355 pbb, sehingga disimpulkan bahwa konsentrasi 355 pbb lebih besar dari sebagian besar data yang ada.
Dengan menggunakan R interval prediksi menggunakan satu sisi dapat dihitung menggunakan fungsi berikut:
PInp_os <- function(x, obs, alpha, side){
# mengurutkan data dari yang terkecil
x_sort = sort(x)
# jumlah observasi
n = length(x)
# rangking observasi
ru = (1-alpha)*(n+1)
ru_1 = ceiling(ru)
ru_2 = floor(ru)
rl = alpha*(n+1)
rl_1 = ceiling(rl)
rl_2 = floor(rl)
# perhitungan interval atas dan bawah
PIup = x_sort[ru_1]+((ru-ru_1)/(ru_2-ru_1))*(x_sort[ru_2]-x_sort[ru_1])
PIdown = x_sort[rl_1]+((rl-rl_1)/(rl_2-rl_1))*(x_sort[rl_2]-x_sort[rl_1])
# decision making
if((side=="upper") & (PIup<obs)){
cat("PI =",PIup,",observasi baru=",obs)
cat("\n----------------------------------------------------------------------")
cat("\nKesimpulan:")
cat("\nnilai observasi lebih besar dibandingkan sebagian besar nilai yang ada")
} else if((side=="lower") & (PIdown>obs)){
cat("PI =",PIdown, ",observasi baru=",obs)
cat("\n----------------------------------------------------------------------")
cat("\nKesimpulan:")
cat("\nnilai observasi lebih kecil dibandingkan sebagian besar nilai yang ada")
} else if(side==""){
print("side belum ditentukan tentukan apakah lower atau upper")
} else{
cat("batas bawah =",PIdown,", batas atas =",PIup)
cat("\n---------------------------------------------------------")
cat("\nKesimpulan:")
cat("\nnilai observasi sama dengan sebagian besar nilai yang ada")
}
}Note:
- x: vektor numerik
- alpha: alpha level yang digunakan
- obs: observasi baru yang akan dibandingkan
- side: untuk memilih jenis uji satu sisi yang digunakan. nilai yang mungkin adalah Upper (membandingkan dengan limit atas) dan Lower (membandingkan dengan limit bawah)
PInp_os(x=gwardat$konsentrasi, obs=355, alpha=0.1, side="upper")## PI = 316 ,observasi baru= 355
## ----------------------------------------------------------------------
## Kesimpulan:
## nilai observasi lebih besar dibandingkan sebagian besar nilai yang ada10.6 Interval Prediksi Parametrik
Interval prediksi parametrik juga digunakan untuk menentukan apakah pengamatan baru kemungkinan berasal dari distribusi yang berbeda dari data yang dikumpulkan sebelumnya. Namun, pada metode parametrik asumsi bentuk dari distribusi data akan diperhitungkan. Asumsi ini memberikan lebih banyak informasi untuk membangun interval, asalkan asumsi tersebut valid. Jika data tidak mengikuti distribusi yang diasumsikan, interval prediksi mungkin tidak akurat.
10.6.1 Interval Prediksi Distribusi Simetris
Asumsi yang digunakan untuk melakukan perhitungan interval prediksi untuk distribusi data yang simetris adalah data haruslah berdistribusi normal. Interval prediksi selanjutnya dibentuk secara simetris pada kedua sisi nilai mean. Interval ini lebih lebar rentangnya dibandingkan dengan interval kepercayaan nilai mean. Persamaan matematis yang digunakan untuk menghitungnya dituliskan pada Persamaan (13).
\[\begin{equation} PI=\overline{X}-t_{\left(\frac{\alpha}{2},n-1\right)}\cdot\sqrt{s^2+\left(\frac{s^2}{n}\right)}sampai\ \overline{X}+t_{\left(\frac{\alpha}{2},n-1\right)}\cdot\sqrt{s^2+\left(\frac{s^2}{n}\right)} \tag{13} \end{equation}\]Untuk interval satu sisi Persamaan (13), menjadi Persamaan (14).
\[\begin{equation} PI=\overline{X}-t_{\left(\alpha,n-1\right)}\cdot\sqrt{s^2+\left(\frac{s^2}{n}\right)}sampai\ \overline{X}+t_{\left(\alpha,n-1\right)}\cdot\sqrt{s^2+\left(\frac{s^2}{n}\right)} \tag{14} \end{equation}\]Untuk lebih memahaminya misalkan terdapat hasil pengukuran baru konsentrasi arsenik sebesar 350 ppb dengan menggunakan data pada Tabel 3 sebagai pembanding. Buktikan bahwa observasi baru tersebut berasal dari distrubusi yang sama dengan \(\alpha\)=5%.
Dengan menggunakan Persamaan (13), interval prediksi dapat dihitung sebagai berikut:
\[ PI\ =\ 98,4-t_{\left(0.025,24\right)}\cdot\sqrt{144,7^2+\frac{144,7^2}{25}\ }sampai\ \ 98,4+t_{\left(0.025,24\right)}\cdot\sqrt{144,7^2+\frac{144,7^2}{25}} \]
\[ PI\ =\ 98,4-2,064\cdot147,6\ \ sampai\ \ 98,4+2,064\cdot147,6 \]
\[ PI\ =\ -206,25\ \ sampai\ \ 403,05 \]
Berdasarkan hasil perhitungan yang dilakukan terlihat bahwa limit interval prediksi yang dihasilkanterdapat nilai negatif. Kosentrasi negatif mengindikasikan bahwa data yang digunakan tidaklah simetris sehingga penggunaan interval prediksi untuk data yang simetris tidak dapat digunakan pada data tersebut. Metode perhitungan interval prediksi untuk data asimetris lebih cocok untuk digunakan.
Pada R interval prediksi disekitar nilai mean dapat dihitung menggunakan fungsi berikut:
PI_sim <- function(x, obs, alpha, side){
# menghitung nilai mean
ave = mean(x, na.rm=TRUE)
# menghitung nilai varians dara
var = var(x, na.rm=TRUE)
# menghitung df
n = length(x)
df = n-1
# perhitungan rentang satu sisi
pi_l1 = ave-qt((1-alpha), df)*sqrt(var+(var/n))
pi_u1 = ave+qt((1-alpha), df)*sqrt(var+(var/n))
# perhitungan rentang dua sisi
pi_l2 = ave-qt((1-alpha/2), df)*sqrt(var+(var/n))
pi_u2 = ave+qt((1-alpha/2), df)*sqrt(var+(var/n))
# decision making
if(side=="upper" & obs>pi_u1){
cat("PI Atas =",pi_u1,",observasi baru=",obs)
cat("\n----------------------------------------------------------------------")
cat("\nKesimpulan:")
cat("\nnilai observasi lebih besar dibandingkan sebagian besar nilai yang ada")
}else if(side=="lower" & obs<pi_l1){
cat("PI Bawah =",pi_l1,",observasi baru=",obs)
cat("\n----------------------------------------------------------------------")
cat("\nKesimpulan:")
cat("\nnilai observasi lebih kecil dibandingkan sebagian besar nilai yang ada")
}else if(side=="two side" & obs>pi_u2){
cat("PI Bawah =",pi_l2,",observasi baru=",obs, ",PI Atas =",pi_u2)
cat("\n----------------------------------------------------------------------")
cat("\nKesimpulan:")
cat("\nnilai observasi lebih besar dibandingkan sebagian besar nilai yang ada")
}else if(side=="two side" & obs<pi_l2){
cat("PI Bawah =",pi_l2,",observasi baru=",obs, ",PI Atas =",pi_u2)
cat("\n----------------------------------------------------------------------")
cat("\nKesimpulan:")
cat("\nnilai observasi lebih kecil dibandingkan sebagian besar nilai yang ada")
}else if(side=="upper" & obs<pi_u1){
cat("PI Atas =",pi_u1,",observasi baru=",obs)
cat("\n----------------------------------------------------------------------")
cat("\nKesimpulan:")
cat("\nnilai observasi sama dengan sebagian besar nilai yang ada")
}else if(side=="lower" & obs>pi_l1){
cat("PI Bawah =",pi_l1,",observasi baru=",obs)
cat("\n----------------------------------------------------------------------")
cat("\nKesimpulan:")
cat("\nnilai observasi sama dengan sebagian besar nilai yang ada")
}else{
cat("PI Bawah =",pi_l2, ",observasi baru=",obs,",PI Atas =",pi_u2)
cat("\n---------------------------------------------------------")
cat("\nKesimpulan:")
cat("\nnilai observasi sama dengan sebagian besar nilai yang ada")
}
}Note:
- x: vektor numerik
- alpha: alpha level yang digunakan
- obs: observasi baru yang akan dibandingkan
- side: untuk memilih jenis uji digunakan. nilai yang mungkin adalah upper (membandingkan dengan limit atas uji satu sisi), lower (membandingkan dengan limit bawah uji satu sisi) dan two side (uji dua sisi).
# interval prediksi satu sisi
PI_sim(x = gwardat$konsentrasi, obs = 350, alpha=0.05, side=2)## PI Bawah = -206.177 ,observasi baru= 350 ,PI Atas = 402.881
## ---------------------------------------------------------
## Kesimpulan:
## nilai observasi sama dengan sebagian besar nilai yang ada10.6.2 Interval Prediksi Untuk Distribusi Data Yang Tidak Simetris
Untuk distribusi data yang tidak simetris, data perlu dilakukan transformasi terlebih dahulu sebelum dilakukan. Data di lingkungan khusunya parameter di air cenderung memiliki bentuk distribusi tidak simetris (cenderung memiliki kemencengan positif). Transformasi logaritmik biasanya dapat digunakan untuk data tersebut agar bentuknya dapat simetris dan dapat memenuhi asumsi normalitas pada data. Data yang telah dilakukan transformasi selanjutnya dihitung menggunakan Persamaan (13) untuk interval prediksi dua sisi dan Persamaan (14) untuk interval prediksi satu sisi. Hasil perhitungan selanjutnya dilakukan transformasi kembali sesuai dengan invers dari transformasinya dalam hal ini menggunakan transformasi eksponensial (jika tranformasi awalnya adalah natural log). Untuk data dengan bentuk distribusi logaritmik (kemencengan positif), interval prediksi yang digunakan disajikan pada Persamaan (15) (dua sisi) dan Persamaan (16) (satu sisi).
\[\begin{equation} PI=\exp\left(\overline{X}-t_{\left(\frac{\alpha}{2},n-1\right)}\cdot\sqrt{s^2+\left(\frac{s^2}{n}\right)}\right)\ sampai\ \exp\left(\overline{X}+t_{\left(\frac{\alpha}{2},n-1\right)}\cdot\sqrt{s^2+\left(\frac{s^2}{n}\right)}\right) \tag{15} \end{equation}\] \[\begin{equation} PI=\exp\left(\overline{X}-t_{\left(\alpha,n-1\right)}\cdot\sqrt{s^2+\left(\frac{s^2}{n}\right)}\right)\ sampai\ \ \exp\left(\overline{X}+t_{\left(\alpha,n-1\right)}\cdot\sqrt{s^2+\left(\frac{s^2}{n}\right)}\right) \tag{16} \end{equation}\]dimana \(y=\ln{(x)}\), \(\overline{y}\) adalah nilai rata-rata dari tranformasi logaritmik data, dan \(s^2_y\) adalah varians dari tranformasi logaritmik data.
Dengan menggunakan contoh soal sebelumnya misalkan terdapat observasi baru konsentrasi arsenik sebesar 350 ppb. Kita perlu menentukan apakah observasi baru tersebut berasal dari distribusi yang sama berdasarkan data pada Tabel 3.
Berdasarkan hasil visualisasi diketahui bahwa distribusi data yang dihasilkan memiliki bentuk kemencengan positif sehingga interval prediksi asimetris dapat digunakan. Dengan menggunakan \(\alpha\)=5% prediksi interval dua sisi dapat dihitung menggunakan Persamaan (15).
\[ \ln\left(PI\right)\ =\ 3,71-t_{\left(0.025,24\right)}\cdot\sqrt{1,96^2+\frac{1,96^2}{25}\ }sampai\ \ 3,71+t_{\left(0.025,24\right)}\cdot\sqrt{1,96^2+\frac{1,96^2}{25}\ } \] \[ \ln\left(PI\right)\ =\ 3,71-2,064\cdot2,11\ sampai\ \ 3,71+2,064\cdot2,11 \]
\[ \ln\left(PI\right)\ =\ -1,19\ \ sampai\ \ 7,53 \]
\[ PI=\ 0,31\ \ sampai\ \ 1476.07 \]
Berdasarkan hasil yang diperoleh diketahui bahwa observasi baru berada diantara rentang tersebut. Rentang yang dihasilkan cukup besar yang disebabkan karena tinkat kepercayaan yang digunakan juga besar (95%). Pembaca dapat juga menggunakan tingkat kepercayaan yang lain seperti 99% dan 90%. Semakin besar alpha yang digunakan interval prediksi yang dihasilkan semakin kecil. Namun perlu diingat bahwa semakin kecil rentangnya maka error (alpha) juga semakin besar.
Pembaca juga dapat menggunakan bentuk transformasi lain untuk membentuk data yang lebih simetris dan memnuhi asumsi distribusi normal. Bentuk transformasi lain akan mengubah bentuk persamaan yang digunakan. Transformasi kuadrat misalnya akan mengubah transformasi pada ersamaan (15) dan Persamaan (16) menjadi akar kuadrat.
Pada R interval prediksi dengan bentuk transformasi data logaritmik dapat dituliskan sebagai berikut:
PI_asim <- function(x, obs, alpha, side){
# transformasi logaritmik (kemencengan positif)
x_trans = log(x)
# menghitung nilai mean
ave = mean(x_trans)
# menghitung nilai varians dara
var = var(x_trans)
# menghitung df
n = length(x)
df = n-1
# perhitungan rentang satu sisi
pi_l1 = exp(ave-qt((1-alpha), df)*sqrt(var+(var/n)))
pi_u1 = exp(ave+qt((1-alpha), df)*sqrt(var+(var/n)))
# perhitungan rentang dua sisi
pi_l2 = exp(ave-qt((1-alpha/2), df)*sqrt(var+(var/n)))
pi_u2 = exp(ave+qt((1-alpha/2), df)*sqrt(var+(var/n)))
# decision making
if(side=="upper" & obs>pi_u1){
cat("PI Atas =",pi_u1,",observasi baru=",obs)
cat("\n----------------------------------------------------------------------")
cat("\nKesimpulan:")
cat("\nnilai observasi lebih besar dibandingkan sebagian besar nilai yang ada")
}else if(side=="lower" & obs<pi_l1){
cat("PI Bawah =",pi_l1,",observasi baru=",obs)
cat("\n----------------------------------------------------------------------")
cat("\nKesimpulan:")
cat("\nnilai observasi lebih kecil dibandingkan sebagian besar nilai yang ada")
}else if(side=="two side" & obs>pi_u2){
cat("PI Bawah =",pi_l2,",observasi baru=",obs, ",PI Atas =",pi_u2)
cat("\n----------------------------------------------------------------------")
cat("\nKesimpulan:")
cat("\nnilai observasi lebih besar dibandingkan sebagian besar nilai yang ada")
}else if(side=="two side" & obs<pi_l2){
cat("PI Bawah =",pi_l2,",observasi baru=",obs, ",PI Atas =",pi_u2)
cat("\n----------------------------------------------------------------------")
cat("\nKesimpulan:")
cat("\nnilai observasi lebih kecil dibandingkan sebagian besar nilai yang ada")
}else if(side=="upper" & obs<pi_u1){
cat("PI Atas =",pi_u1,",observasi baru=",obs)
cat("\n----------------------------------------------------------------------")
cat("\nKesimpulan:")
cat("\nnilai observasi sama dengan sebagian besar nilai yang ada")
}else if(side=="lower" & obs>pi_l1){
cat("PI Bawah =",pi_l1,",observasi baru=",obs)
cat("\n----------------------------------------------------------------------")
cat("\nKesimpulan:")
cat("\nnilai observasi sama dengan sebagian besar nilai yang ada")
}else{
cat("PI Bawah =",pi_l2, ",observasi baru=",obs,",PI Atas =",pi_u2)
cat("\n---------------------------------------------------------")
cat("\nKesimpulan:")
cat("\nnilai observasi sama dengan sebagian besar nilai yang ada")
}
}Note:
- x: vektor numerik
- alpha: alpha level yang digunakan
- obs: observasi baru yang akan dibandingkan
- side: untuk memilih jenis uji digunakan. nilai yang mungkin adalah upper (membandingkan dengan limit atas uji satu sisi), lower (membandingkan dengan limit bawah uji satu sisi) dan two side (uji dua sisi).
# interval prediksi satu sisi
PI_asim(x = gwardat$konsentrasi, obs = 350, alpha=0.05, side=2)## PI Bawah = 0.386043 ,observasi baru= 350 ,PI Atas = 1476.073
## ---------------------------------------------------------
## Kesimpulan:
## nilai observasi sama dengan sebagian besar nilai yang ada10.7 Interval Kepercayaan Persentil
Kuantil atau persentil telah digunakan secara tradisional dalam sumber daya air untuk menggambarkan frekuensi kejadian banjir. Dengan demikian banjir 100 tahun adalah persentil ke-99 (0,99 kuantil) dari distribusi puncak banjir tahunan. Besarnya banjir yang diperkirakan hanya akan dilampaui sekali dalam 100 tahun. Banjir 20 tahun besarnya besarnya yang diperkirakan hanya akan dilampaui sekali dalam 20 tahun (5 kali dalam 100 tahun), atau merupakan persentil ke-95 dari puncak tahunan. Demikian pula, banjir 2 tahun adalah median atau persentil ke-50 dari puncak tahunan. Persentil banjir ditentukan dengan asumsi bahwa aliran puncak mengikuti distribusi yang ditentukan seperti distribusi Log Pearson type III atau distribusi Gumbel.
Interal kepercayaan persentil berbeda dengan interval kepercayaan median. Hal yang paling jelas terlihat adalah interval kepercayaan persentil mengukur interval kepercayaan pada setiap persentil data yang ada, sedangkan intervak kepercayaan media hanya mengukur pada lokasi pusat data atau persentil ke-50.
Interval kepercayaan persentil juga disebut sebagai interval toleransi. Nilai persentil digunakan sebagai koefisien cakupan dari interal toleransi. Pada chapter ini akan dibahas lebih jauh mengenai metode perhitungan interval toleransi baikdengan metode parametrik maupun dengan metode nonparametrik.
10.7.1 Interval Kepercayaan Nonparametrik Persentil
Metode perhitungan interval kepercayaan nonparametrik persentil mirip dengan perhitungan interval kepercayaan median. Kita akan menggunakan kembali tabel binomial jika sampel kita kecil untuk menentukan limit atas dan bawah yang merupakan nilai kritis dari alpha yang telah kita tetapkan. Nilai kritis ini selanjutnya akan ditransformasikan kedalam bentuk rangking pada data yang menunjukkan titik observasi ujung pada interval kepercayaan.
Tabel binomial dimasukkan pada kolom dengan nilai \(p\), persentil yang diinginkan interval kepercayaannya. Jadi untuk interval kepercayaan pada persentil ke-75, kolom \(p=0,75\) digunakan. Cari pada baris kolom tersebut sampai \(n\) dengan probabilitas mendekati alpha level (\(\alpha/2\)) ditemukan. Nilai kritis \(x_l\) bawah adalah bilangan bulat yang sesuai dengan probabilitas \(p^*\). Nilai kritis kedua \(x_u\) juga diperoleh dengan melanjutkan pada kolom tersebut sampai menemukan probabilitas \(p'=\left(1-\frac{\alpha}{2}\right)\). Nilai kritis \(x_l\) dan \(x_u\) digunakan untuk menghitung rangking \(R_l\) dan \(R_u\) yang sesuai dengan nilai data di ujung atas dan bawah limit kepercayaan (Persamaan (17) dan Persamaan (18)). Level interval kepercayaan yang dihasilkan akan sama dengan \(\left(p'-p\cdot\right)\).
\[\begin{equation} R_l=x_l+1 \tag{17} \end{equation}\] \[\begin{equation} R_u=x_u \tag{18} \end{equation}\]Untuk memahami mengenai penerapan interval kepercayaan persentil diberikan sebuah contoh kita diminta untuk menentukan 95% interval kepercayaan nilai persentil ke-20 (\(C_{0.20}\)) data konsentrasi arsenik pada Tabel 3 (p=0,2).
Berdasarkan data pada Tabel 3, nilai persentil ke-20 (\(\overline{C}_{0.20}\))= 3.36ppb, yaitu data yang berada pada rangking 0,2*(26)=5,2 atau dua per sepuluh jarak antara data ke-5 dan ke-6. Untuk menentukan rentang kepercayaan persentil ke-20 sebenarnya dari data, kita perlu menggunakan kembali tabel binomial dengan menginputkan nilai p=0,2. nilai kritis \(x_l\) diperoleh dengan mencari probabilitas data pada kolom p=0,2 yang mendekati nilai \(\alpha/2\)=0,025 adalah 1 (\(p'\)=0,027, error probabilitas sisi bawah distribusi). Dengan menggunakan Persamaan (17), diperoleh \(R_l=2\). Dengan cara sama untuk sisi atas distribusi nilai kritis atas \(x_u\) diperoleh dengan menginputkan nilai p=0,20 dengan nilai probabilitas mendekati \(1-\frac{\alpha}{2}\)= 0,975 diperoleh sebesar 9 (\(p'\)=0,983, error probabilitas sisi atas distribusi). Sehingga rentang kepercayaang 95,6% (0,983-0,027=0,956) untuk persentil ke-20 berada pada range data dengan rangkin ke-2 dan ke-9, atau
\[ 1,5\le C_{0.20}\le8\ pada\ \alpha=0,044 \]
Jika data yang kita miliki cukup besar dengan jumlah sampel \(n>20\) (sebagian buku menyebutkan \(n>30\)), kita dapat menggunakan distribusi normal untuk memperkirakan rentang kepercayaan persentil.Persamaan yang digunakan untuk menentukan batas atas dan bawah disajikan pada Persamaan (19) dan Persamaan (20).
\[\begin{equation} R_l=np+z_{\frac{\alpha}{2}}\cdot\sqrt{np\left(1-p\right)}+0,5 \tag{19} \end{equation}\] \[\begin{equation} R_l=np+z_{\left[1-\frac{\alpha}{2}\right]}\cdot\sqrt{np\left(1-p\right)}+0,5 \tag{20} \end{equation}\]Dengan menggunakan contoh sebelumnya kita dapat menghitung kembali rentang kepercayaan 95% persentil ke-20 menggunakan Persamaan (19) dan Persamaan (20) diperoleh rangking data batas bawah dan atas sebagai berikut:
\[ R_l=25\cdot0,2+\left(-1,96\right)\cdot\sqrt{25\cdot0,2\left(1-0,2\right)}+0,5\ =\ 5-1,96\cdot2+0,5=1,6 \]
\[ R_u=25\cdot0,2+1,96\cdot\sqrt{25\cdot0,2\left(1-0,2\right)}+0,5\ =\ 5+1,96\cdot2+0,5=9,4 \]
Berdasarkan hasil perhitungan diperoleh rangking data batas bawah dan batas atas secara berurutan adalah data ke-2 (batas bawah) dan data-9 (batas atas). Hasil yang diperoleh ini sama dengan yang telah diperoleh sebelumnya.
Pada R kita dapat membentuk fungsi untuk menghitung interval kepercayaan persentil sesuai dengan yang kita inginkan seperti lokasi persentil yang ingin kita uji serta jenis uji yang digunakan berdasarkan jumlah sampel yang kita inputkan. Selain itu rentang kepercayaan ini dapat pula digunakann untuk menghitung rentang kepercayaan median atau persentil ke-50.
CI_npPercent <- function(x, p, alpha){
# jumlah observasi
n = length(x)
# mengurutkan data
x = sort(x)
# membuat vektor yang akan menyimpan
# hasil loop
bl = rep(NA,n)
bu = rep(NA,n)
# decision makin
if(n<= 20){
# looping
for(i in 1:n){
bl[i] = pbinom(i, n, p)
if(b>alpha/2){
break
}
}
for(i in 1:n){
bu[i] = pbinom(i, n, p)
if(b>(1-(alpha/2))){
break
}
}
# menghitung selisih terhadap alpha
dbl = abs(alpha-bl)
dbu = abs(alpha-bu)
# mencari titik kritis
min_bl = which.min(dbl)
min_bu = which.min(dbu)
# menhitung rangking nilai bawah dan atas
rl = min_bl + 1
ru = min-bu
# mencari data sesuai rangking bawah dan atas
LCI = x[rl]
UCI = x[ru]
}else{
# menghitung rangking nilai bawah dan atas
rl = (n*p)+qnorm(alpha/2)*sqrt((n*p)*(1-p))+0.5
ru = (n*p)+(qnorm(1-(alpha/2))*sqrt((n*p)*(1-p)))+0.5
# mencari data sesuai rangking bawah dan atas
LCI = x[floor(rl)]+
((rl-floor(rl))/(ceiling(rl)-floor(rl)))*(x[ceiling(rl)]-x[floor(rl)])
UCI = x[floor(ru)]+
((ru-floor(ru))/(ceiling(ru)-floor(ru)))*(x[ceiling(ru)]-x[floor(ru)])
}
cat("Lower CI=", LCI," <= C(", p, ") <= ",
"Upper CI=", UCI)
}Note:
- x: vektor numerik.
- p: persentil yang ingin dicari. Nilai berkisar antara 0 sampai 1.
- alpha: alpha level yang digunakan.
Pembaca dapat menjalankan fungsi tersebut mengggunakan data pada contoh soal sebelumnya yaitu mencari interval kepercayaan persentil ke-20. Jalankan sintaks berikut untuk mengetahui hasil yang diperoleh.
CI_npPercent(x= gwardat$konsentrasi, p= 0.2, alpha=0.05)10.7.2 Uji Nonparametrik Untuk Persentil
Pengujian persentil dilakukan untuk mengecek apakah sebuah persentil berbeda (lebih besar atau lebih kecil) dibandingkan dengan sejumlah nilai. Sebagai contoh misalkan terdapat median kualitas harian suatu parameter tidak boleh melebihi standar yang berlaku sebesar \(X_0\) ppb. Contoh lain dalam bidang hidrologi periode ulang hujan (PUH) 10 tahun atau persentil ke-90 dari debit puncak tahunan suatu kawasan dapat dilakukan pengujian apakah nilai yang ada dilapangan berbeda dengan PUH 10 tahunan yang telah kita hitung untuk digunakan dalam mendesain saluran drainase. Pembahasan pengujian persentil tersebut tidak akan sampai menyinggung pengujian hipotesis yang akan dibahas pada Chapter selanjutnya. Pembahasan akan berkisar membandingkan suatu nilai dengan interval kepercayaan seperti yang telah dijelaskan pada pembahasan terkait interval prediksi.
Pengujian apakah sebuah nilai \(X_0\) berbeda dengan sejumlah rentang nilai yang ditetapkan dapat dilakukan dengan pengujian dua sisi dan satu sisi. Pengujian satu sisi melihat apakah suatu nilai \(X_0\) berada diluar interval kepercayaan persentil atau diantara nilai batas bawah \(X_l\) dan nilai batas atasnya \(X_u\) (lihat Gambar 10). Sedangkan pengujian satu sisi melihat apakah suatu nilai lebih besar atau lebih kecil (tergantung apakah pengujian satu sisi sebelah atas distribusi atau sebelah bawah distribusi) dari interval kepercayaan persentil yang digunakan (lihat Gambar 11 dan Gambar 12).

Figure 10: Interval estimasi persentil Xp sebagai penguji apakah Xp=X0. A) X0 didalam interval estimasi sehingga Xp tidak berbeda secara signifikan dari X0, B) X0 berada diluar rentang estimasi sehingga Xp berbeda secara signifikan dari X0. (Helsel dan Hirsch, 2002)

Figure 11: Interval estimasi persentil Xp sebagai penguji apakah Xp>X0. A) X0 didalam interval estimasi sehingga Xp tidak signifikan lebih besar dari X0, B) X0 berada diluar rentang estimasi sehingga Xp signifikan lebih besar dari X0. (Helsel dan Hirsch, 2002)

Figure 12: Interval estimasi persentil Xp sebagai penguji apakah Xp>X0. A) X0 didalam interval estimasi sehingga Xp tidak signifikan lebih kecil dari X0, B) X0 berada diluar rentang estimasi sehingga Xp signifikan lebih kecil dari X0. (Helsel dan Hirsch, 2002)
Untuk menghitungnya secara nonparametrik menggunakan Persamaan (19) dan Persamaan (20) untuk jumlah sampel kecil sedangkan untuk sampel besar kita dapat menggunakan Persamaan (19) dan Persamaan (20).
Dengan menggunakan kembali data pada Tabel 3 kita akan menghitung apakah kadar arsenik kualitas air tanah tersebut melebihi baku mutu arsenik pada air minum dengan baku mutu konsentrasi arsenik tidak melampaui 300 ppb. Dengan menggunakan nilai \(\alpha\)=0,05 dan batas bawah persentil yang digunakan sebagai acuan pembanding adalah persentil ke-90 dapat dihitung sebagai berikut:
\[ \overline{C}_{0.90}=\left(25+1\right)\cdot0,9=23,4\ \left(data\ point\right)=300+0,4\left(340-300\right)=316\ ppb \] Karena jumlah sampel lebih besar dari 20, maka kita dapat menghitung batas atas data menggunakan Persamaan (20).
\[ R_l=np+z_{0,05}\sqrt{np\left(1-p\right)}=25\cdot0,9+\left(-1,64\right)\cdot\sqrt{2,25}+0,5=20,5 \] Kita dapat membulatkan hasilnya menjadi observasi 20 atau 21. Interpolasi linier dapat dilakukan sehingga diperoleh nilai observasi sebesar 215 ppb. Nilai ini lebih kecil dibandingkan \(X_0\)=300 ppb, sehingga baku mutu arsenik belum terlampaui oleh kualitas air tanah tersebut.
Kita dapat menggunakan fungsi CI_npPercent() untuk menghitung rentang persentil yang kita inginkan. Untuk pengujian satu sisi nilai alpha yang akan diinputkan perlu dikali oleh dua karena fungsi tersebut pada dasarnya digunakan untuk menghitung rentang kepercayaan persentil secara nonparametrik (nilai alpha dibagi pada kedua sisi). Berikut adalah contoh sintaks untuk menguji apakah sampel yang kita miliki melebihi baku mutu (persentil ke-90 dan alpha=5%):
CI_npPercent(gwardat$konsentrasi, 0.9, 0.1)10.7.3 Interval Kepercayaan Parametrik Untuk Persentil
Interval kepercayaan untuk persentil juga dapat dihitung dengan mengasumsikan bahwa data mengikuti distribusi tertentu. Asumsi distribusi digunakan karena sering ada data yang tidak cukup untuk menghitung persentil dengan presisi yang diperlukan. Menambahkan informasi yang terkandung dalam distribusi akan meningkatkan ketepatan estimasi selama asumsi distribusi masuk akal. Namun ketika distribusi yang diasumsikan tidak sesuai dengan data dengan baik, estimasi yang dihasilkan kurang akurat, dan lebih menyesatkan, daripada jika tidak ada yang diasumsikan. Sayangnya, situasi di mana asumsi paling dibutuhkan ketika ukuran sampel yang kecil, adalah situasi yang sama di mana sulit untuk menentukan apakah data mengikuti distribusi yang diasumsikan.
Pada interval kepercayaan parametrik asumsi terhadap kecocokan data terhadap suatu distribusi perlu diperhatikan. Data di lingkungan umumnya memiliki bentuk distribusimengikuti distribusi lognormal. Selain itu, distribusi yang sering sekali digunakan adalah distribusi Pearson Tipe III dan Gumbel. Kedua pendekatan distribusi tersebut akan mempengaruhi metode perhitungan yang digunakan. Sehingga pengetahuan yang lebih baik mengenaik distribusi tersebut diperlukan. Pada buku ini kita hanya akan membahas mengenai perhitungan interval kepercayaan menggunakan distribusi lognormal. Pembaca dapat membaca mengenai penerapan distribusi lainnya melalui junal yang ditulis oleh Wei dan Song (2019).
Perhitungan estimasi titik dan interval untuk persentil dengan asumsi distribusi lognormal dapat dilakukan dengan mudah. Pertama sampel rata-rata \(y\) dan sampel simpangan baku \(s_y\) logaritma dihitung. Estimasi titik kemudian dihitung menggunakan Persamaan (21).
\[\begin{equation} X_p=\exp\left(\overline{y}+z_p\cdot s_y\right) \tag{21} \end{equation}\]dimana \(z_p\) merupakan kuantil ke-\(p\) dari distribusi normal standard dan \(y=\ln{(x)}\).
Estimasi interval untuk median sebelumnya diberikan pada Persamaan (7) dengan asumsi bahwa data mengikuti distribusi lognormal. Untuk persentil lainnya, interval kepercayaan dihitung menggunakan distribusi t non-sentral (Stedinger, 1983). Tabel distribusi itu ditemukan dalam artikel Stedinger, dengan list yang lebih lengkap terdapat pada perpustakaan online atau perangkat lunak matematika. Interval kepercayaan pada \(X_p\) dihitung menggunakan Persamaan (22).
\[\begin{equation} CI\left(X_p\right)=\exp\left(\overline{y}+\zeta_{\frac{\alpha}{2}}\cdot s_y,\ \overline{y}+\zeta_{\left[1-\frac{\alpha}{2}\right]}\cdot s_y\right) \tag{22} \end{equation}\]dimana \(\zeta{\alpha/2}\) merupakan \(\alpha/2\) dari kuantil distribusi t non-sentral untuk persentil dengan ukuran sampel \(n\) yang diinginkan.
Untuk lebih memahami penerapannya pembaca dapat mengerjakan contoh soal pada bagian sebelumnya. Dengan menggunakan estimasi interval 90% kita perlu menentukan interval estimasi persentil ke-90 dari data konsentrasi arsenik dengan asumsi distribusi yang digunakan berupa distribusi lognormal.
Dengan menggunakan Persamaan (21) estimasi titik persentil ke-90 dapat dihitung.
\[ C_{0,90}=\exp\left(3,17+1,28\cdot1,96\right)=292,6\ ppb \] Nilai tersebut lebih rentanh dibanding estimasi konsentrasi sebelumnya asumsi data mengikuti distribusi lognormal dengan konsentrasi persentil ke-90 arsenik sebesar 316 ppb.
Dengan menggunakan Persamaan (22), interval kepercayaan 90% dapat dihitung.
\[ \exp\left(3,17+0,898\cdot1,96\right)<C_{0,90}<\exp\left(3,17+1,838\cdot1,96\right) \]
\[ 138,4<C_{0,90}<873,5 \]
10.7.4 Uji Parametrik Untuk Persentil
Seperti pada bagian sebelumnya kita ingin melihat apakah persentil dari sekumpulan data berbeda dengan nilai tertentu (dapat berupa baku mutu). Pengujian dilakukan dengan melihat apakah nilai tertentu tersebut berada diantara interval kepercayaan persentil dari data (uji dua sisi), lebih besar atau lebih kecil dari batas bawah atau batas atas interval kepercayaan persentil (uji satu sisi). Langkah pengujian dilakukan sama dengan sebelumnya dengan menghitung terlebih dulu batas atas atau batas bawah persentil data yang selanjutnya dibandingkan dengan nilai tertentu.
Dengan menggunakan hasil dari perhitungan sebelumnya, dengan menggunakan alpha=0,05 kita perlu menentukan apakah batas bawah interval kepercayaan melampaui baku mutu arsenik sebesar 300 ppb (uji satu sisi). Berdasarkan hasil perhitungan diperoleh batas bawah interval kepercayaan persentil ke-90 sebesar 138,4 ppb atau lebih kecil dibandingkan batas yang ditentukan, sehingga disimpulkan bahwa konsentrasi arsenik persentil ke-90 pada data tidak melampaui baku mutu yang ditentukan.
10.8 Interval Kepercayaan Menggunakan Metode Bootstrap
Bootstrap merupakan metode inferensi populasi menggunakan data sampel. Metode ini dikembangkan oleh Bradley Efron pada tahun 1979. Jika pembaca ingin lebih mengenal metode ini pembaca dapat membaca makalahnya di tautan berikut. Pembaca dapat membaca makalah tersebut secara gratis.
Bootstrap mengandalkan pengambilan sampel dengan pengembalian dari data sampel. Teknik ini dapat digunakan untuk memperkirakan standard error (se) dari setiap statistik dan untuk memperoleh interval kepercayaan (CI) untuk itu. Bootstrap sangat berguna ketika CI tidak memiliki bentuk tertutup, atau memiliki bentuk yang sangat rumit.
Misalkan kita memiliki sejumlah sampel dengan ukuran \(n\): \(X=\left\{x_1,x_2,...,x_n\right\}\) dan kita tertarik dengan CI dari beberapa statistik data \(T=t\left(X\right)\). Metode ini sangat mudah untuk dikerjakan. Kita hanya perlu mengulang sejumlah \(R\) kali skema berikut: Untuk pengulangan ke-\(i\), sampling dengan pengembalian \(n\) data dari data sampel yang tersedia. Namai sampel baru tersebut sebagai sampel bootstrap ke-\(i\) , \(X_i\), dan hitung statistik (mean, median atu persentil) yang ingin dihitung interval kepercayaannya.
Sebagai hasilnya, kita akan mendapatkan nilai R dari statistik yang telah kita hitung: \(T_1,T_2,\ ....,\ T_R\). Kita dapat menyebutnya sebagai realisasi bootstrap dari \(T\) atau distribusi bootstrap dari \(T\). Berdasarkan hal tersebut, kita dapat menghitung CI untuk T.
Pada contoh kali ini penulis akan menyajikan cara melakukan bootstrap untuk menghitung interval kepercayaan pada mean, median, dan persentil. Data yang penulis gunakan adalah data gwardat pada Tabel 3.
Bootstrap pada R dilakukan dengan menggunakan library boot. Berikut adalah contoh pertama menghitung interval kepercayaan median:
# memuat paket
library(boot)# membuat hasil yang diperoleh lebih random
# dan reproducible
set.seed(100)
# membuat fungsi boot
med.boot.func <- function(x,i){
median(x[i])
}
# melakukan bootstrap
median.boot <- boot(gwardat$konsentrasi,
# memasukkan fungsi boot
med.boot.func,
# menentukan jumlah replikasi
R=1000)
# print hasil
median.boot##
## ORDINARY NONPARAMETRIC BOOTSTRAP
##
##
## Call:
## boot(data = gwardat$konsentrasi, statistic = med.boot.func, R = 1000)
##
##
## Bootstrap Statistics :
## original bias std. error
## t1* 19 9.2795 27.3119Berdasarkan hasil yang diperoleh diketahui bahwa median dataset original sebesar 19. Pada hasil juga diperoleh nilai bias bootstrap. Nilai bias tersebut merupakan selisih dari nilai rata-rata 1000 median hasil bootstrap dikurangi dengan median sampel keseluruhan (original median). Standard error merupakan standard deviasi dari 1000 median yang terhitung.
Untuk mengetahui distribusi sampling yang telah kita lakukan. kita dapat melihat distribusi dengan mengeplotkan semua sampel bootstrap pada histogram dan QQ-plot dengan menjalankan sintaks berikut:
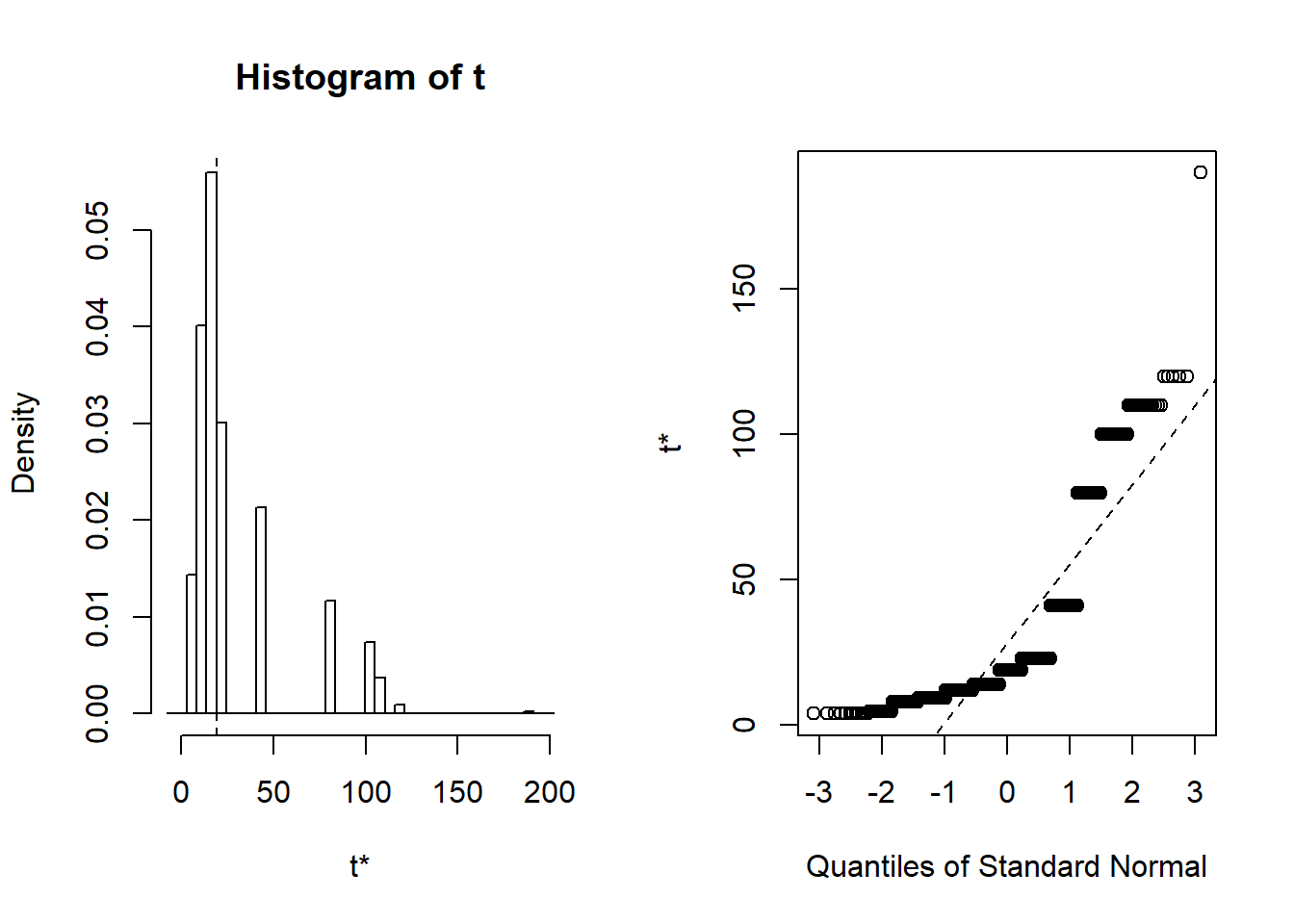
Figure 13: Distribusi bootstrap median
Berdasarkan Gambar 13 diketahui bahwa median tidak berdistribusi normal. Hal ini ditunjukkan dari distribusi pada histogram yang membentuk kemencengan positif. Selain itu, distribusi data pada QQ-plot juga tidak mengikuti garis referensi yang ada sehingga dapat disimpulkan bahwa distribusi median bootstrap tidak berdistribusi normal.
Untuk menghitung interval kepercayaan median dengan tingkat kepercayaan 95%, kita dapat menggunakan fungsi boot.ci(). Berikut adalah sintaks yang digunakan:
boot.ci(boot.out=median.boot, conf=0.95)## Warning in boot.ci(boot.out = median.boot, conf = 0.95): bootstrap
## variances needed for studentized intervals## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 1000 bootstrap replicates
##
## CALL :
## boot.ci(boot.out = median.boot, conf = 0.95)
##
## Intervals :
## Level Normal Basic
## 95% (-43.81, 63.25 ) (-72.00, 33.20 )
##
## Level Percentile BCa
## 95% ( 4.8, 110.0 ) ( 4.8, 100.0 )
## Calculations and Intervals on Original ScaleTerdapat 4 buah hasil dari 4 buah metode yang dihasilkan sebagai output fungsi tersebut. Metode Normal mengasumsikan distribusi median bootstrap berdistribusi normal. Berdasarkan hasil visualisasi yang diperoleh diketahui bahwa distribusi data cenderung memiliki kemencengan positif sehingga metode ini tidak dapat digunakan, Selain itu, rentang yang dihasilkan juga terdapat nilai negatif yang mustahik dihasilkan pada konsentrasi arsenik (sebagian besar parameter lingkungan memiliki nilai terkecil \(\le0\)). Metode Basic memiliki asumsi bahwa tidak ada bias antara median data dengan median rata-rata hasil bootstrap. Berdasarkan hasil perhitungan yang dilakukan terlihat bahwa terdapat bias pada hasil bootstrap yang cukup besar sehingga metode ini tidak dapat diterapkan. Metode ketiga adalah metode persentil. Metode ini mengasumsikan bahwa distribusi median simetris, yang telah disinggung sebelumnya bahwa distribusi median tidak simetris sehingga metode ini tidak dapat diterapkan pada kasus ini. Metode terakhir adalah metode BCa (bias-corrected and accelerated) mengoreksi bias dan membuat lebih sedikit asumsi. Metode ini akan sering banyak kita gunakan pada data kita. Berdasarkan seluruh hasil yang telah diperoleh dapat kita simpulkan bahwa metode BCa cukup baik dalam menjelaskan interval kepercayaan median. Selain itu, metode persentil juga mempunyai hasil yang relatif mirip dengan BCa meskipun dari asumsi yang digunakan keempat metode tersebut tidak ada yang terpenuhi.
Pesan peringatan dalam output hasil menunjukkan bahwa interval kepercayaan kelima, disebut sebagai studentized interval, tidak dapat dihitung karena varians untuk sampel bootstrap tidak disediakan. Interval kepercayaan studentized berusaha untuk mengoreksi bias dengan “studentizing” setiap median yang dihitung (misal: mengurangi rata-rata median dan kemudian membaginya dengan standard error). Tampaknya tidak ada rumus umum untuk menghitung standard error untuk median, tetapi ada pedoman dalam literatur untuk memperkirakan kesalahan standar ketika populasi data yang mendasarinya diasumsikan terdistribusi secara normal. Dalam contoh ini, interval BCa tampaknya cukup baik. Perhatikan bahwa dalam beberapa kasus, mungkin ada peringatan bahwa “beberapa interval BCa mungkin tidak stabil.” Dalam hal itu, hasil BCa harus diabaikan jika intervalnya tampak tidak masuk akal, dan pilihan dibuat dari opsi lain yang tersisa, berdasarkan pada Ulasan histogram dan plot probabilitas estimasi bootstrap.
Setelah pembaca memahami prosedur melakukan bootstrap pada median, pembaca dapat melakukan bootstrap pada persentil dan mean. Untuk bootstrap mean jalankan sintaks berikut:
# membuat hasil yang diperoleh lebih random
# dan reproducible
set.seed(100)
# membuat fungsi boot
mean.boot.func <- function(x,i){
mean(x[i])
}
# melakukan bootstrap
mean.boot <- boot(gwardat$konsentrasi,
# memasukkan fungsi boot
mean.boot.func,
# menentukan jumlah replikasi
R=1000)
# print hasil
mean.boot##
## ORDINARY NONPARAMETRIC BOOTSTRAP
##
##
## Call:
## boot(data = gwardat$konsentrasi, statistic = mean.boot.func,
## R = 1000)
##
##
## Bootstrap Statistics :
## original bias std. error
## t1* 98.352 -1.396536 27.84389Distribusi mean bootstrap disajikan pada Gambar 14
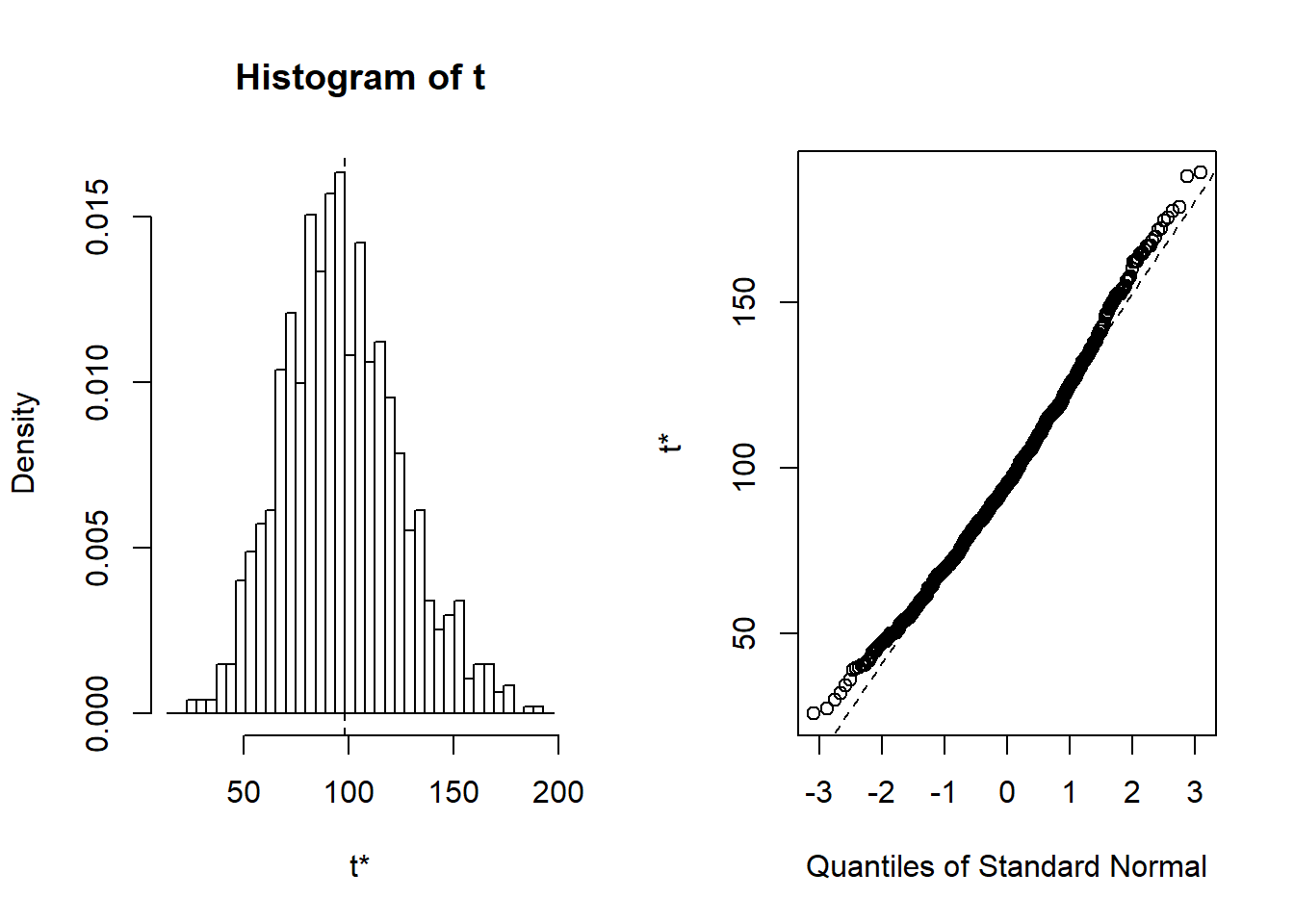
Figure 14: Distribusi bootstrap mean
Berdasrkan hasil yang diperoleh, distribusi mean bootstrap mengikuti distribusi normal. Untuk memperoleh interval kepercayaan mean bootstrap jalankan sintaks berikut:
boot.ci(boot.out=mean.boot, conf=0.95)## Warning in boot.ci(boot.out = mean.boot, conf = 0.95): bootstrap variances
## needed for studentized intervals## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 1000 bootstrap replicates
##
## CALL :
## boot.ci(boot.out = mean.boot, conf = 0.95)
##
## Intervals :
## Level Normal Basic
## 95% ( 45.18, 154.32 ) ( 39.21, 149.05 )
##
## Level Percentile BCa
## 95% ( 47.66, 157.50 ) ( 56.43, 175.06 )
## Calculations and Intervals on Original Scale
## Some BCa intervals may be unstableBerdasarkan hasil yang diperoleh dapat dilihat bahwa metode BCa tidak dapat digunakan karena hasil yang diperoleh tidak stabil, Ketiga metode lainnya dapat digunakan karena asumsi normalitas (simetri) terpenuhi. Selain itu bias yang dihasilkan relatif kecil sehingga metode Basic juga dapat digunakan.
Bootstrap terkahir yang kita lakukan adalah untuk memperoleh interval kepercayaan persentil dalam hal ini penulis akan mencobanya dengan persentil ke-90. Berikut alah sintaks yang digunakan:
# membuat hasil yang diperoleh lebih random
# dan reproducible
set.seed(100)
# membuat fungsi boot
p90.boot.func <- function(x,i){
quantile(x[i], probs=0.9)
}
# melakukan bootstrap
p90.boot <- boot(gwardat$konsentrasi,
# memasukkan fungsi boot
p90.boot.func,
# menentukan jumlah replikasi
R=1000)
# print hasil
p90.boot##
## ORDINARY NONPARAMETRIC BOOTSTRAP
##
##
## Call:
## boot(data = gwardat$konsentrasi, statistic = p90.boot.func, R = 1000)
##
##
## Bootstrap Statistics :
## original bias std. error
## t1* 280 -0.9156 85.66162Visualisasi distribusi bootstrap persentil 90 disajikan pada Gambar 15
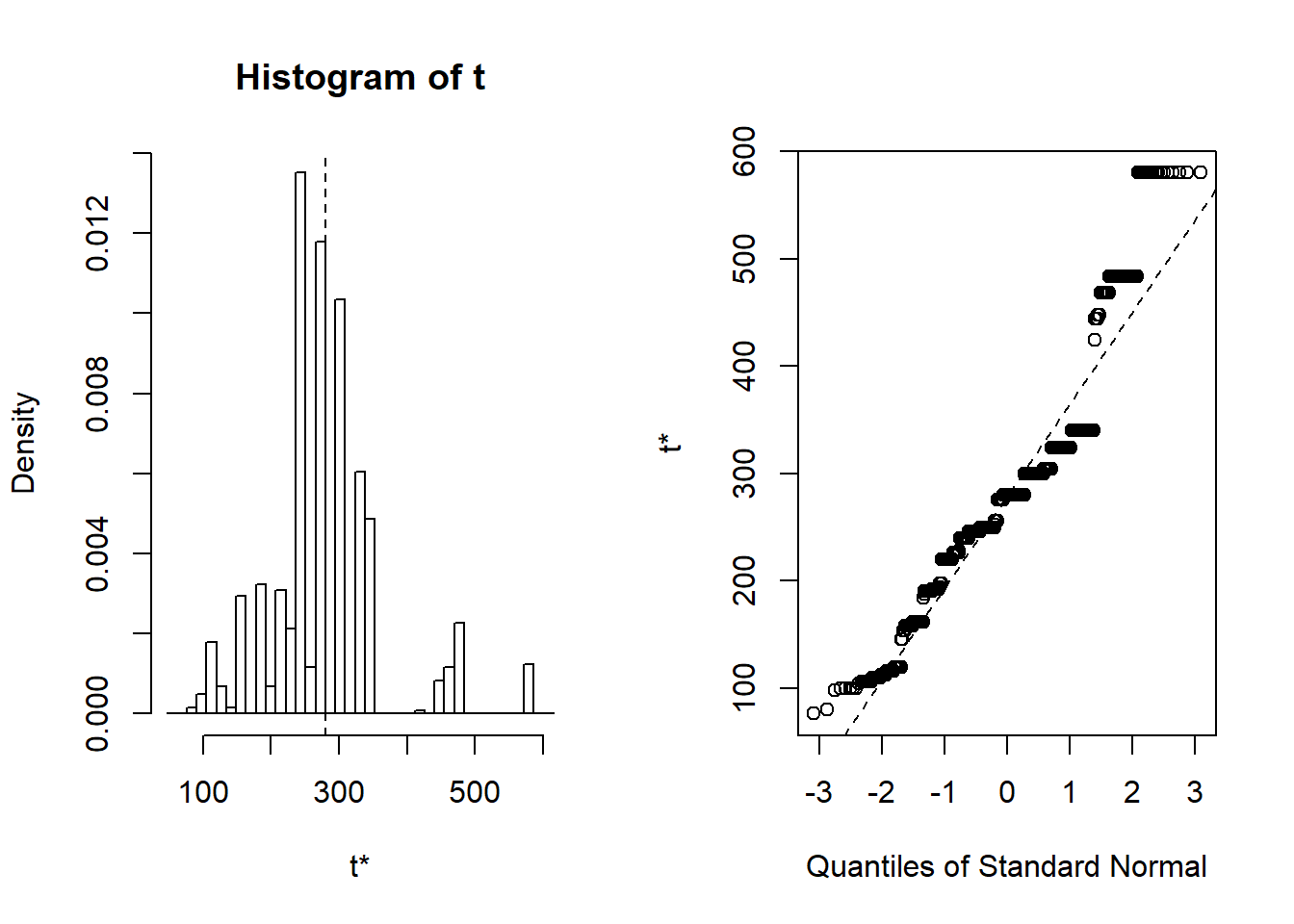
Figure 15: Distribusi bootstrap persentil 90
Bentuk visualisasi distribusi bootstrap persentil ke-90 yang dihasilkan pada Gambar 15 terlihat sedikit memiliki kemencengan positif. untuk menghitung interval kepercayaan 95% persentil ke-90 jalankan sintaks berikut:
boot.ci(boot.out=p90.boot, conf=0.95)## Warning in boot.ci(boot.out = p90.boot, conf = 0.95): bootstrap variances
## needed for studentized intervals## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 1000 bootstrap replicates
##
## CALL :
## boot.ci(boot.out = p90.boot, conf = 0.95)
##
## Intervals :
## Level Normal Basic
## 95% (113.0, 448.8 ) ( 76.0, 448.0 )
##
## Level Percentile BCa
## 95% (112, 484 ) (120, 580 )
## Calculations and Intervals on Original ScaleBerdasarkan keempat hasil yang diperoleh, metode BCa cukup baik digunakan sebab distribusi bootstrap yang dihasilkan tidak memenuhi asumsi ketiga metode lainnya.
10.9 Kegunaan Lain Dari Interval Kepercayaan
Selain digunakan untuk menghitung interval estimasi, interval kepercayaan dapat pula digunakan sebagai pendeteksi adanya outlier, kontrol kualitas, dan penentuan ukuran sampel yang akan digunakan pada suatu penelitian agar hasil yang diperoleh lebih presisi. Pembahasan juga akan disertai apakah normalitas pada distribusi data akan mempengaruhi performa dari ketiga jenis kegunaan interval kepercayaan.
10.9.1 Implikasi Non-Normalitas Pada Pendeteksian Outlier
Outlier merupakan pengamatan yang tampak berbeda karakteristiknya dibandingkan sebagian besar pengamatan yang ada. Pengamatan ini seringkli dihapus dari prosedur analisis yang mengharuskan distribusi suatu data mengikuti distribusi normal. Penghapusan observasi ini bisa jadi tidak baik dilakukan sebab bisa saja observasi tersebut valid. Observasi yang bersifat outlier bisa jadi merupakan observasi terpenting sebab bisa saja dapat memberikan gambaran penting pada suatu kondisi ekstrim atau hubungan kausatif yang penting. Penghapusan ini tidak perlu dilakukan selam prosedur pengukuran yang sejenis tersedia dan tidak mengharuskan suatu distribusi data mengikuti distribusi tertentu, meskipun terdapat kelebihan dan kekurangan yang perlu kita perhatikan.
Untuk menghapus observasi yang kita identifikasikan sebagai outlier, aturan atau tes perlu dilakukan seperti tes yang diajukan oleh Beckman dan Cook (1983). Tes yang paling umum didasarkan pada interval-t, dan mengasumsikan data mengikuti distribusi normal. Biasanya Persamaan (13) untuk interval pediksi data yang mengikuti distribusi normal disederhanakan dengan mengabaikan nilai \(\frac{s^2}{n}\). Nilai diluar interval prediksi tersebut selanjutnya dapat dinyatakan sebagai oulier. Uji lain yang dapat dilakukan adalah dengan visualisasi menggunakan box plot. Nilai diluar \(Q1-1,5IQR\) atau \(Q3+1,5IQR\) dinyatakan sebagai outlier. Namun pada Chapter ini tidak akan dibahas lebih lanjut sebab pada Chapter 7 telah dibahas mengenai deteksi outlier mellaui visualisasi data.
10.9.2 Implikasi Non-Normalitas Pada Kontrol Kualitas
Presentasi visual interval kepercayaan yang digunakan secara luas dalam proses industri adalah kontrol chart. Sejumlah kecil produk disampel dari total kemungkinan pada titik waktu tertentu, dan rerata dihitung. Pengambilan sampel diulang pada interval reguler atau acak, tergantung pada desain, menghasilkan serangkaian cara sampel. Ini digunakan untuk membangun satu jenis kontrol chart, xbar chart. Chart ini secara visual mendeteksi ketika rata-rata sampel masa depan menjadi berbeda dari yang digunakan untuk membangun grafik. Keputusan perbedaan didasarkan pada melebihi interval kepercayaan parametrik di sekitar rata-rata yang telah dijelaskan dibagian lain Chapter ini.
Misalkan laboratorium kimia mengukur larutan standar yang sama beberapa kali selama sehari untuk menentukan apakah peralatan dan operator menghasilkan hasil yang konsisten. Untuk serangkaian pengukuran \(n\) pada interval waktu \(m\), ukuran sampel total \(N=N\cdot M\). Perkiraan konsentrasi terbaik untuk standar itu adalah rata-rata keseluruhan yang dihitung menggunakan Persamaan (23).
\[\begin{equation} \overline{X}=\sum_{i=1}^N\frac{X_i}{N} \tag{23} \end{equation}\]\(\overline{X}\) diplot sebagai garis tengah grafik. Interval kepercayaan pada rata-rata tersebut dijelaskan oleh Persamaan (8), menggunakan ukuran sampel \(n\) yang tersedia untuk menghitung setiap nilai rata-rata individu. Batas interval tersebut juga diplotkan sebagai garis paralel pada chart kontrol kualitas. Nilai rata-rata yang akan berada diluar batas plot rata-rata ini hanya sebesar \(\alpha\cdot100\%\) dari waktu jika rata-rata berditribusi normal. Observasi yang berada di luar batas lebih sering daripada ini diambil untuk menunjukkan bahwa sesuatu dalam proses telah berubah.
Jika \(n\) besar (katakanlah 30 atau lebih), Teorema Limit Pusat menyatakan bahwa rata-rata akan terdistribusi secara normal meskipun data yang mendasarinya mungkin tidak. Namun jika \(n\) jauh lebih kecil, seperti yang sering terjadi, berarti mungkin tidak mengikuti pola ini. Khususnya, untuk data yang memiliki kemencengan (data dengan outlier hanya pada satu sisi), distribusi di sekitar rata-rata mungkin masih memiliki kemencengan. Hasilnya adalah nilai besar untuk simpangan baku, dan pita kepercayaan yang lebar. Oleh karena itu, chart akan memiliki kekuatan yang lebih rendah untuk mendeteksi observasi yang mulai menjauh dari nilai rata-rata yang diharapkan daripada jika data tidak memiliki kemencengan.
Chart kontrol juga diproduksi untuk menggambarkan varians proses. Chart kontrol juga menggunakan nilai range (R chart) atau simpangan baku (S chart). Kedua grafik bahkan lebih sensitif terhadap perubahan data dari kondisi normal dibandingkan \(\overline{X}\) chart. Keduanya akan mengalami kesulitan dalam mendeteksi perubahan varian ketika data yang mendasarinya tidak normal, dan ukuran sampel \(n\) untuk setiap rata-rata kecil.
10.9.3 Non-Normalitas Terhadap Desain Sampling
Persamaan t-interval juga digunakan untuk menentukan jumlah sampel yang diperlukan untuk memperkirakan rata-rata dengan tingkat presisi yang ditentukan. Namun, persamaan tersebut membutuhkan data untuk kira-kira mengikuti distribusi normal. Persamaan tersebut harus mempertimbangkan power serta lebar interval. Artinya kita harus memutuskan apakah mean adalah karakteristik yang paling tepat untuk mengukur data yang memiliki kemencengan.
Untuk memperkirakan ukuran sampel telah cukup untuk menentukan interval estimasi dengan lebar spesifik dapat menggunakan Persamaan (24).
\[\begin{equation} n=\left(\frac{t_{\frac{\alpha}{2},n-1}\cdot s}{\Delta}\right)^2 \tag{24} \end{equation}\]dimana \(s\) merupakan simpangan baku sampel dan \(\Delta\) merupakan setengah lebar interval yang diinginkan. Seperti yang telah dibahas di atas, untuk ukuran sampel kurang dari 30 hingga 50 dan bahkan lebih besar dengan data yang sangat menceng, perhitungan ini mungkin memiliki kesalahan besar. Perkiraan \(s\) akan tidak akurat, dan akan sangat sangat meningkat nilainya karena kemencenga dan/atau outlier apapun. Karenanya, estimasi \(n\) yang dihasilkan akan besar. Sebagai contoh, Hakanson (1984) memperkirakan jumlah sampel yang diperlukan untuk memberikan lebar interval yang masuk akal untuk karakteristik sedimen sungai dan danau, termasuk kimia sedimen. Berdasarkan koefisien variasi yang dilaporkan dalam artikel, data untuk sedimen sungai cukup menceng, seperti yang mungkin diharapkan. Ukuran sampel yang diperlukan untuk sungai dihitung pada 200 dan lebih tinggi.
Sebelum menggunakan persamaan sederhana seperti itu, data yang menceng harus ditransformasi terlebih dahulu sehingga lebih simetris, jika bukan berdistribusi normal. Misalnya, logaritma akan secara drastis menurunkan taksiran ukuran sampel untuk data miring, setara dengan Persamaan (15). Ukuran sampel akan dihasilkan yang memungkinkan median (rata-rata geometris) diperkirakan dalam faktor toleransi multiplikasi sama dengan \(\pm2\Delta\)dalam satuan log.
Masalah kedua dengan Persamaan (24) untuk memperkirakan ukuran sampel, bahkan ketika data mengikuti distribusi normal, ditunjukkan oleh Kupper dan Hafner (1989). Mereka menunjukkan Persamaan (24) meremehkan ukuran sampel sebenarnya yang diperlukan untuk tingkat presisi tertentu, bahkan untuk perkiraan \(n\le40\). Hal ini disebabkan karena Persamaan (24) tidak mengakui bahwa simpangan baku \(s\) hanya estimasi dari nilai sebenarnya \(\sigma\). Mereka menyarankan menambahkan probabilitas toleransi ke Persamaan (24), mirip dengan statement of power. Maka perkiraan lebar interval setidaknya sekecil lebar interval yang diinginkan untuk beberapa persentase tertentu (katakanlah 90 atau 95%) dari waktu tersebut. Misalnya, ketika \(n\) akan sama dengan 40 berdasarkan Persamaan (24), lebar interval yang dihasilkan akan lebih kecil dari lebar yang diinginkan \(2\Delta\) hanya sekitar 42% dari waktu. Ukuran sampel seharusnya menjadi 53 untuk memastikan lebar interval berada dalam kisaran toleransi 90% dari waktu.
Ukuran sampel yang diperlukan untuk estimasi interval median atau untuk melakukan tes nonparametrik dari Chapter selanjutnya dapat diturunkan tanpa asumsi normalitas yang diperlukan di atas untuk interval-t. Noether (1987) menjelaskan estimasi ukuran sampel yang lebih kuat ini, yang memasukkan pertimbangan power sehingga lebih valid daripada Persamaan (24). Namun, baik estimasi normalitas distribusi data atau nonparametric mempertimbangkan efek penting dan sering diamati dari musiman atau tren, dan karenanya mungkin tidak pernah memberikan perkiraan yang cukup akurat untuk menjadi sesuatu yang lebih dari sekadar panduan kasar.
Referensi
- Bachman, L. J. 1984. Field and laboratory analyses of water from the Columbia Aquifer in Eastern Maryland. Ground Water 22. 460-467.
- Damanhuri, E. 2011. Statitika Lingkunga. Penerbit ITB.
- Deryto, T. tanpa tahun. Bootstrap in R. Datacamp. https://www.datacamp.com/community/tutorials/bootstrap-r
- Efron, B. 1979. Bootstrap Methods: Another Look at The Jacknife. The Annuals of Statistics. Vol:7(1). 1-26.
- Helsel, D.R., Hirsch, R.M. 2002. statistical Methods in Water Resources. USGS.
- Kupper, L. L., and K. B. Hafner. 1989. How appropriate are popular sample size formulas?. American Statistician 43. 101-105.
- Noether, G. E. 1987. Sample size determination for some common nonparametric tests. Journal American Statistical Assoc.. 82, 645-647.
- Ofungwu, J. 2014. Statistical Applications For Environmental Analysis and Risk Assessment. John Wiley & Sons, Inc.
- Ting Wei, Songbai Song. 2019. Confidence interval estimation for precipitation quantiles based on principle of maximum entropy. Entropy. 21.